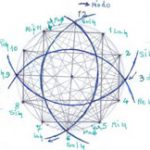
«ارتعاشاتی مکانیکی که در محیطی ارتجاعی منتشر می شوند»؛ این تعریفی است از «صوت». حال اگر این صوت دارای ارتعاشی ثابت و منظم باشد، «نت موسیقایی» خواهد بود. اگر دو ارتعاش صوت به طور هم زمان به گوش انسان برسند، بسته به نسبت فرکانس دو ارتعاش، گوش احساس ملایمت (Consonance) یا عدم ملایمت (Dissonance) خواهد کرد. هر چه نسبت فرکانسی دو صوت، به صورت یک کسر ساده تر باشد، برای گوش ملایم تر خواهد بود. با نواختن یک نت موسیقی، «هارمونیک»هایی به گوش خواهد رسید که هارمونیک های دورتر از نت اصلی ناملایم تر می شوند.
اینها اصولی ساده و اولیه از فیزیک صوت هستند. همین اصول ساده «هری پاچ» (Harry Partch) را ترغیب به جستجوی منشاء موسیقی کرد. وی از ۲۴ ژوئن ۱۹۰۱ تا ۳ سپتامبر ۱۹۷۴ زیست. پدر و مادرش مبلغین مذهبی یکی از فرقه های یهودی بودند. شاید همین موجب شد تا در سال ۱۹۴۷، به تقلید از تورات، مهم ترین اثر مکتوبش را «کتاب آفرینش موسیقی» نام گذارد. این کتاب به واسطه بررسی هایی که پاچ روی فواصل موسیقی انجام داده است، دارای اعتبار است.
هری پاچ با الهام از مطالعات آکوستیکی «هرمان فون هلمولتز»، فیزیک صوت را سنگ بنای محکمی برای موسیقی می دانست. از این رو وی سیستم تعدیل یافته ۱۲-ET را یک «انحراف بزرگ» و موسیقی کلاسیک را دارای «ریشه ای ضعیف» می دانست. هم چنین وی عقیده داشت «فیثاغورث» با استفاده از تنها یک هارمونیک (۲/۳) از بعضی فواصل ملایم دور شده است. برای نمونه فیثاغورث با استفاده از چهار چرخه فاصله پنجم، نسبت ۶۴/۸۱ را برای فاصله سوم بزرگ پیشنهاد کرده که به عقیده پاچ چون فاصله ۴/۵ ملایم تر است، فیثاغورث از فواصل صحیح موسیقی عدول کرده است.
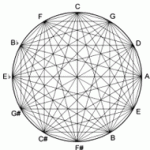
هری پاچ «تک صدایی» (monophony) را راه رسیدن به فواصل صحیح موسیقی می دانست. وی عقیده داشت با پایه قرار دادن نسبت ۱/۱ و استفاده از سری هارمونیک ها، می توان سیستمی از فواصل ملایم تشکیل داد. برای این کار وی فواصل را در دو دسته جای داد: ۱- فوق نغمگی (over-tonality یا به اختصار otonality) ؛ ۲- مادون نغمگی (under-tonality یا به اختصار utonality). منظور از فوق نغمگی فواصلی است که در سری هارمونیک نت پایه و منظور از مادون نغمگی فواصلی است که در سری زیرهارمونیک نت پایه ایجاد می شوند. پس باید گفت دسته نت های مادون نغمگی، معکوس فواصل فوق نغمگی است. به همین جهت بر خلاف فوق نغمگی، دسته نت های مادون نغمگی یک پدیده آکوستیکی طبیعی نیستند.
به بیان ریاضی می توان این دو دسته را به تصاعد حسابی مربوط دانست. تصاعد حسابی n اٌم یک سری از اعداد با توجه به جمله m اٌم و قدر نسبت d از رابطه زیر محاسبه می شود:
تذکر: عنوان این مطلب به نگاه فیثاغوریان به اعداد اشاره دارد، چنانچه شعار مدرسه فیثاغورث «همه چیز اعداد است» بوده.




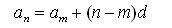


































بسیاااااااااار عــــــــــــالی
MAS
با سپاس فراوان