نظری به دسته ‏بندی وزن‏ ها در موسیقی موزون (۷)

نگاهی متفاوت به دسته‏ بندی وزن ‏ها
من در اینجا برای به دست دادن دسته ‏بندی دقیق‏ تر از وزن‏ های موسیقی موزون فرضیه ‏سازی‏ ای‏ انجام داده ‏ام که ماحصلِ «استنتاج از راه بهترین تبین» (باجینی ۱۳۹۴: ۱۹) است و تا تبینی روشن‏ تر، جامع و مانع ‏تر می‏ تواند معتبر باشد. بنابراین دسته ‌بندی ‌ای که در اینجا پیشنهاد می ‌شود وزن ‌ها را به این دسته ‌ها ‌ تقسیم می ‌کند: الف- انواع وزن بر مبنای تعداد ضرب در سلول ‌های وزنی (میزان) (۱۱) شامل انواع وزن یک ضربی تا بیش از ۱۲۰ ضربی (۱۲) ب- انواع وزن بر مبنای نوع تقسیم ضرب به این صورت: دوتایی (ساده) (۱۳) سه ‌تایی (ترکیبی)؛ پنج ‌تایی (پنج جزئی )؛ هفت ‌تایی(هفت جزئی) و…؛ ج- انواع وزن بر مبنای اجتماع ضرب ‌ها یعنی کنار هم قرارگیری انواع ضرب ‌ها به این صورت تک ‌زمانه: با امتداد برابر، دوزمانه: با دو امتداد متفاوت و چند زمانه: با چند امتداد مختلف؛ که دراین صورت وزن ‌های تک زمانه «سالم یا متقارن» و وزن ‌های دو و چند زمانه از نوع «لنگ یا نامتقارن» محسوب می ‌شوند. یادآوری می کنم که کلمه ‌ی لنگ (Aksak) عیناً در فرهنگ موسیقی کلاسیک ترکی وجود و به همین منظور کاربرد دارد (Tanrıkorur 2014: 34؛ Reinhard 2007: 65؛Toussaint 2013: 40؛ Duygulu 2014: 36) د- انواع وزن بر مبنای اجتماع وزن ‌هایی با تعداد ضرب متفاوت֯ که در سنت موسیقی خاورمیانه به عنوان «ایقاع مرکب» شناخته می ‌شده است (ابن ‌سینا ۱۳۹۴: ۱۳۱-۱۳۲).

شایان ذکر است من در این دسته ‌بندی وزن ‌هایی را که به نام متبادل (Alternating)(Pearsall2012:168) یا ترکیب ‌شده (Combined) (رید ۱۳۹۴: ۲۳۷)معرفی شده ‌اند را تعمداً کنار گذاشته ‌ام زیرا هر سلول وزنی (پریود متریک) به صورت مستقل وجود دارد و تغییر الگوی وزنی منجر به تغییر وزن می ‌شود و هیچ وزنی نمی ‌تواند تبدیل به وزنی دیگر شود مگر با تغییر الگوییِ وزنی ‌ای که آنرا پدید آورده است که در این صورت دیگر آن وزن قبلی نیست.

در ضمن مساوی بودن مجموع مقدار امتدادهای دو سلول وزنی مختلف دلیل کافی برای متبادل دانستن دو وزن متفاوت نیست. چنین خطایی ناشی از خلط مفهوم ریتم و متر است و مصداق وزن ‌های مختلط است. نکته ‌ی اخیر شامل فنون بسط و گسترش و یا ایجاد وزن ‌های متنوع از پایه ‌های وزنی مشخص، مانند برخی از آنچه فارابی برای ایجاد تغییر در وزن آورده است (ساوا ۱۳۸۲: ۷۲-۷۵)، نخواهد بود.  

پی نوشت
۱۱- لازم به یادآوری است که مبحث دیگری که اغلب با سلول ‌های وزنی خلط می ‌شود پریودهای متریک- ریتمیک ثابتی است که با عناوین «دور ایقاعی، اصول و یا مدهای ریتمیک Rhythmic Modes و الگوهای ریتمیک Rhythmic Patterns» شناخته می ‌شوند. این اشکال نیز از عدم تفکیک صحیح وزن و ریتم در ذهن است (Hasty 1997:3-13 و Kvifte2007: 66).

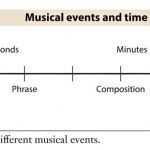
۱۲- اگر چه در عمل مغز انسان از تعدادی محدود، به بالا در اجتماع ضرب ‌ها، سلول وزنی را تقسیم به دسته ‌های کوچکتر کرده و درک می ‌کند. یک دلیل در این مورد عدم توانایی حفظ دور طویل (سلول وزنی بلند) در حافظه ‌ی بشر است (پوپل۱۳۸۹: ۶۵-۸۰) که البته در این زمینه فاصله ‌های زمانی متفاوتی ذکر شده است ولی به هر حال از ۱۵ ثانیه فراتر نمی ‌رود (Collins 2010: 289). استدلال محدودیت درک زمان حال֯ نافی وجود سلول ‌های وزنی بیش از چهار نیست. در این زمینه همچنین نک. کُردمافی۱۳۹۳: ۱۱۹-۱۶۴.

۱۳- در مورد وزن ‌هایی که واحد وزنی آنها دارای تقسیمات دوتایی و یا سه تایی هستند چنان که می ‌دانیم به ترتیب اصطلاح ‌های ساده و ترکیبی هم به کار می ‌رود.