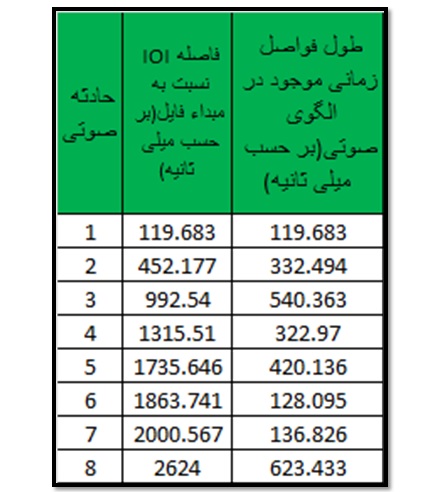
طول زمان یک الگوی تکرار شونده در این صدای ریتمیک معادل ۲.۶۴۲ ثانیه است. در این الگو ۸ حادثه صوتی که دارای منشا مکانیکی یکسانی هستند وجود دارد. این منشا همچنان که قبلا گفته شد احتمالا ناشی از اصطکاک و خرابی در اجزاء داخلی پله برقی است. با بررسی نمودار فرکانس – زمان، طول زمان ۸ حادثه صوتی طبق جدول زیر به دست می آید:
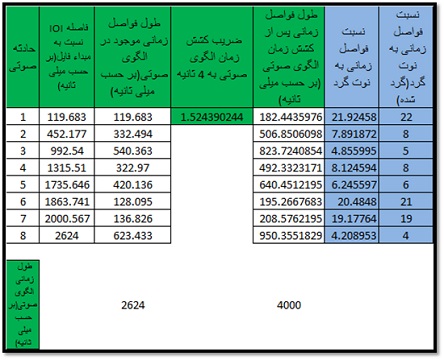
این فواصل در زمانی معادل ۲.۶۲۴ ثانیه توزیع شده اند. حال سوال این است که این فواصل را چگونه باید نشان داد. برای پاسخ می توان طول الگوی زمانی را بر اساس ضریبی افزایش داده تا به ۴ ثانیه برسد. بدیهی است که در این کشیدگی و بر اساس ضریب کشش، طول تمام فواصل زمانی به طور متناسب افزایش پیدا می کند. در این مورد ضریب کشش زمانی معادل ۱.۵۲۴۳ است.
مزیت این کار این است که اندازه تمام فواصل زمانی بر اساس نوت گرد به دست می آید و چون سیستم فواصل زمانی که در تئوری رایج موسیقی ارائه می شود بر مبنای تقسیمات نوت گرد است به این ترتیب می توان مقایسه خوبی را بین فواصل زمانی انجام داد. در نهایت اندازه فواصل زمانی با توجه به ضریب کشش و نسبت فواصل زمانی نسبت به نوت گرد (با فرض تمپو مساوی ۶۰) در یک الگوی صوتی ۴ ثانیه ای طبق جدول زیر به دست می آید:
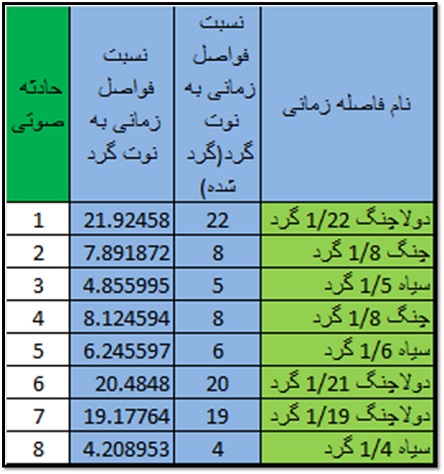
در جدول بالا نسبت فواصل زمانی را گرد کردم و از اعشار صرف نظر نمودم، بنابراین نسبتی مانند ۷.۹۴ به ۸ تبدیل می شود. این گرد شدگی در واقع نوعی اعتدال فواصل زمانی می باشد. البته می توانستم چنین نکرده و نسبت واقعی را در نظر بگیرم. بر اساس آنچه در بالا مشاهده می کنیم می توان فواصل زمانی را چنین نامید:
در زیر هم نوت نویسی الگوی صوتی مشاهده می شود:
اعداد زیرهرنوت نشان دهنده نسبت آن با نوت گرد می باشد. مثلا عدد۲۲ در زیر دولاچنگ یعنی دولاچنگی که نسبت ۲۲/۱ با نوت گرد دارد. حال با آگاهی ازاین که الگوی ما تکرار شونده بوده و الگوی ریتمیک- صوتی آن نیز تقریبا ثابت است واین دو عامل نشانه ای از وجود وزن موسیقایی می باشند، باید سوال کرد کسر میزان وزن این الگو چیست؟
با توجه به متنوع بودن فواصل زمانی در این الگوی صوتی و نبود یک فاصله زمانی در سطح “Beat Level” برای مشخص نمودن کسر میزان چاره ای جز در نظر گرفتن کوچکترین مضرب مشترک بین نسبت های فواصل زمانی نداریم. بین اعداد ۲۰،۱۹،۴،۶،۵،۸،۲۲ کوچکترین مضرب مشترک معادل عدد ۲۵۰۸۰ است. برای محاسبه کسر میزان با تقسیم عدد ۲۵۰۸۰ بر تمام نسبت ها و جمع حاصل این تقسیم ها به کسر میزان ۲۵۰۸/۲۵۴۵ می رسیم:
کسر میزان ۲۵۰۸/۲۵۴۵ به نظر عجیب می آید ولی درواقع باید بپذیریم که مقوله زمان موسیقایی از نگاه ریاضی صرفا ساختارهای ساده متریک را در بر نمی گیرد. در جایی که کسر میزان ۱۶/۱۷ یعنی «۱۷تا یک شانزدهم نوت گرد»، کسر میزان ۲۵۰۸/۲۵۴۵ نیز به همین ترتیب تفسیر می شود. اصطلاح کسر میزان موسیقایی از دید ریاضی واقعا یک کسر است چرا که همانطور که قبلا گفتیم، کسر میزان ۱۶/۱۷ یعنی «۱۷تا یک شانزدهم نوت گرد».
طول میزان بر اساس نسبتهای فوق الذکر معادل ۴.۰۵۹۰۱۱ ثانیه بوده و مقدار کسر میزان به مقدار بسیار اندکی (۰.۰۱۴۷ ثانیه) از ۱ بزرگتر است که این تفاوت به دلیل گرد کردن نسبت های زمانی می باشد. وزن ۲۵۰۸/۲۵۴۵ وزنی نامتعارف است. بعدا در نوشته ای جدا در باره اوزان نامتعارف خواهم نوشت.
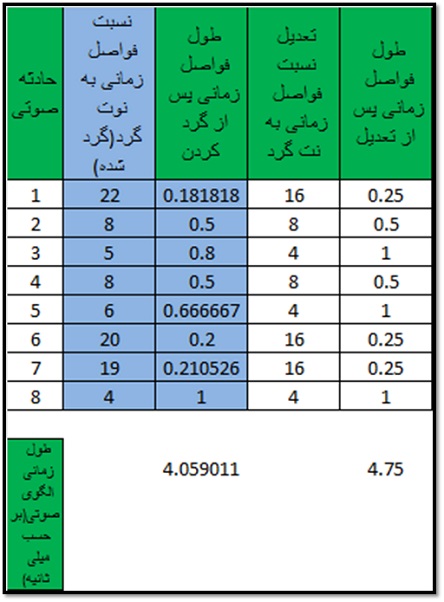
حال ممکن است این ایده به ذهن فردی برسد که آیا می توان این اندازه ها را به شکل دیگری تعدیل کرد؟ تعدیل دراینجا می تواند در واقع به عنوان تبدیل نسبت زمانی موجود به نزدیکترین نسبت زمانی در سیستم نوت نویسی رایج فرض شود. با در نظر گرفتن این فرض می توان تغییرات زیر را انجام داد:
در این روش تعدیل، وزن جدید ما ۱۶/۱۹ خواهد شد. طول زمان این وزن جدید از وزن ۲۵۰۸/۲۵۴۵ به اندازه ۰.۶۹۰۹۸۹ ثانیه بیشتر است. این تفاوت تقریبا نسبتی از نوت گرد معادل ۵۸/۱۰ نوت گرد است.
در زیر فایل صوتی را می شنوید که توسط نرم افزار “Soundforge” ساخته شده و ابتدای آن صدای پله برقی بوده سپس الگوی ساخته شده بر اساس وزن ۲۵۰۸/۲۵۴۵ و در انتها هم الگوی ساخته شده بر اساس وزن ۱۶/۱۹ قرار دارد:
اینجا نمونه صوتی دوم را
بشنوید.
نرم افزازهای مورد استفاده:
۱- TF32
۲- Soundforge



















۱ نظر