بنابر عقیده پیروان مکتب فیثاغورث، اعداد، عناصر اصلی طبیعت و اساس همه چیز بودند، تمام افلاک یک مقیاس موسیقی داشتند که در آن همه چیز با یک هارمونی الهی در جریان است و «موسیقی گردون» را ایجاد میکردند. تصویر مقابل، آخرین درک گرافیکی این نقطه نظر را نشان میدهد که توسط Robert Fludd در سال ۱۶۳۷–۱۵۴۷ در Utriusque Cosmi Historia ترسیم شده است.
یکی از پیروان مشهور فیثاغورث به نام Philolaos به همراه استاد خود در تصویر مطلب قبل نشان داده شده که در حال آزمایش فلوتهایی هستند که دارای نسبت های مختلف می باشند، چکیدهای از عقاید آنها در باب کلیت و جامعیت اعداد به این شرح است: اگر به واسطه وجود اعداد و ماهیت آنها نبود؛ موجودیت هیچ چیز به خودی خود یا در رابطه با سایر اشیا، برای هیچ کس به وضوح مشخص نمی شد.
میتوانید قدرت و نیروی کاربرد اعداد را نه تنها در امور مربوط به نیرو های ماوراءالطبیعه، بلکه در تمام کارها و افکار بشری در کلیه هنرهای دستی و موسیقی مشاهده نمایید.
یکی دیگر از اکتشافات فیثاغورث که برای ما دارای اهمیت است، تئوری تناسب است که دربرگیرنده سه مفهوم، حساب، هندسه و هارمونیک میباشد. اگرچه تئوری تناسبات فیثاغورث برای مقادیر و حجمهای متناقض کاربرد نداشته و آنها را توجیه نمیکند (منظور مقادیری است که به صورت منطقی با اعداد قابل توجیه و تفسیر نیستند) ولی درعین حال، چنانکه شاهد بودهایم، پیروان فیثاغورث وجود آنها را تصدیق کرده اند، بنابراین تصور میشود که آنها این پدیدهها را به عنوان «ضد اعداد» در نظر می گرفتند که به یک بی نظمی و هرج و مرج بدوی و غیر قابل درک تعلق داشتند و به لحاظ ریاضی آنها را «خارج از قلمرو» و شامل مفهوم مهیب بیکرانگی و لایتناهی بودن قلمداد میکردند.
وارث مسلم ریاضیات فیثاغورثیان، افلاطون بود که اگر چه در نزد ما بیشتر به لحاظ نوشتههای فلسفیاش اهمیت دارد، اما پایهگذار آکادمی مشهوری نیز بوده که به جهت اعتبار در زمینه ریاضیات توانسته میان فیثاغورث و هندسهدانان پس از وی از دانشگاه Alexandria و نیز دانشمندان عصر رنسانس یک حلقه ارتباطی برقرار کند. چنانکه میدانیم شعار مشهور این آکادمی از این قرار بوده، «کسی که چیزی از ریاضیات نمیداند اجازه ورود به این مکان را ندارد.» که این اصل بعدها توسط Copernicus (در چرخش کرات آسمانی – ۱۵۴۳) و Leonardo-Trattato della pittura در پیشگفتار کتاب مذکور تأیید و منتشر گردید.
میتوان گفت افلاطون در راستای عقاید ریاضی خود بیشتر از فیثاغورث به مکتب فیثاغورثی پای بند بوده، چرا که در عقاید افلاطونی، نیروی برتر هوش بشری برای این اعتقاد راسخ که طبیعت دقیقاً بر طبق تناسبات ریاضی تنظیم شده، اهمیت بیشتری قائل بود.
این تفکر، افلاطون را به جستجوی طبیعت فراتر از درک و شهود، طبیعت ایدهآل، حقیقتِ واقعیت و «واقعیترین موجودیت» رهنمون کرد. در حالی که فیثاغورث با اعداد کشف شده در هارمونی موسیقی سروکار داشت، افلاطون با اعتقاد به این نکته که دانش باید از احساسات مجزا شود، در خلال یک «سلسله روابط علت و معلول»، به جستجوی هارمونیهای اعداد و هارمونیهای شنیداری که تنها از طریق ذهن قابل درکاند پرداخت.
طبق نظر افلاطون،
تمام چیزهای این جهان کپیهای فانی و ناتمامی از قالبهایی هستند که در جایی وجود خارجی دارند؛ و این قالبها حقیقی و تنها اهداف علوم میباشند، اما تنها از طریق شهود و تأمل مستقیم و بیواسطه ذهنی و عقلانی قابل درک هستند و تا حد امکان از هر گونه نقص های مغشوش کننده در جهان فیزیکی، مجزا و مستقل میباشند.
بدون شک، در جریان اصلی مورد بحث ما مهمترین کاری که افلاطون انجام داده تحقیق وی تحت عنوان Timaeus میباشد که یکی از دو اثر مکتوب بسیار مهم عصر باستان نیز است، کتابی که به زبان لاتین، در قرون وسطی یعنی زمانی که مسیحیان خالق آن را، به آفریدگار تکوین تشبیه میکردند، در اختیار افکار اروپائیان قرار داشت.
Timaeus یک تجسم رسمی از کیهانشناسی عددیِ فیثاغورث – افلاطون است، یعنی همان ماهیتی که در بالا به صورت اجمالی به آن اشاره کردیم. در تشریحِ عناصر و ساختار «روح هستی»، افلاطون اجزای سازنده آن را بر طبق هارمونی اعداد ۱، ۲، ۳، ۴، ۹، ۸ و ۲۷ توضیح میدهد که مجموعهای هستند از مجذورها و توانهای سوم از نسبتهای دو و سه تایی، که از عدد ۱ آغاز شده و به صورت دو تصاعد هندسی ۸، ۴، ۲، ۱ و ۲۷، ۹، ۳،۱ می باشد.
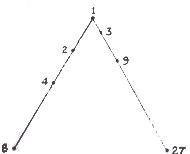
این اعداد که اغلب در آرایش Lambda دیده می شوند (تصویر مقابل)، به همان میزان که در هارمونی الهی نقش دارند در کلیه نسبتهای موسیقی موجود نیز ایجاد هماهنگی میکنند. اعداد طرح های دوبعدی و اجسام سه بعدی، مجذورهای ۴ و ۹ و نیز توانهای سوم ۸ و ۲۷ می باشند.
افلاطون بیشتر از این در یک تئوری اتومیک اسرارآمیز توانست ثابت کند که اصول هندسی چطور می توانند در جاودانگی عالم وجود کاربرد داشته باشند. در این تئوری ۵ عنصر وجود دارد که به صورت حجمهای واقعی هستند که هر کدام از آنها برای بدست آوردن شکل شان ذره ای از آن عنصر را می گیرند. پنجمین حجم افلاطون dodecahedron است که لزوماً از ۲ نوع مثلث اصلی افلاطون ساخته نشده است که در این عالم وجود، برای آراستن صورت آسمانی در کل فلک مورد استفاده قرار می گرفته است. تصاویر این عناصر واقعی در تصویر مقابل آورده شده است.

کتاب مهم دیگر یونان باستان که به تحقیق ما مربوط بوده و نیز بیشترین تأثیر در شکلدهی فرهنگ ما را داشته، کتاب مشهور «اصول اقلیدسی» Elements of Euclid میباشد. در این شاهکار یکپارچه سازی علم ریاضی یونان دیده می شد که رسالهای معتبر در زمینه هندسه برای ۲۰۰۰ سال متمادی به شمار می رفت و چنان منسجم و منطقی جمعآوری و ارایه شد که به جهت دسته بندی منظم و معقول مندرجات موجود در آن، بیشترین تأثیرگذاری را در پیشرفت فرهنگ گذاشت.
در حقیقت، این رساله شامل سیزده کتاب است، که ۶ فصل نخست و ۳ فصل پایانی آن به هندسه اختصاص دارد (سطوح و احجام)، فصل های ۷، ۸ و ۹ مربوط به علم حساب و فصل ۱۰ نیز در باب اعداد گنگ میباشد. عنوان این کتاب یعنی کلمه «اصول»، برطبق یک تفسیر باستانی به معنای «ابتدای ابتدا» به کار رفته است، که در آن اقلیدس تعاریف و قواعد کلی را بیان کرده و خواص و ویژگیهای نقاط، خطوط، سطوح و اشکال را شرح می دهد و آنها را طوری تنظیم و تهیه کرده که به عنوان حقایق غیرقابل بحث و کاملاً مستدل مورد پذیرش می باشند و موضوعات و قضایای حاصل از آنها، نیز به طور منطقی کل ساختار سیستم هندسه را شکل میدهند.
در بخش پنجم این مجموعه تئوری تناسب هم به صورت متناسب وهم به صورت متناقض توضیح داده شده که به یکی از اساتید ریاضی و نجوم به نام Eudoxus of Cnidus منسوب است. وی در این بخش چندین قضیه در باب مقطع طلایی یک خط را نیز شرح داده است. موفقیت و اعتبار این «اصول» از سه جهت بود:
نخست آنکه این کتاب اطلاعات هندسی یونان باستان را در یک قالب منسجم و قابل دسترسی ارایه می کرد، این اطلاعات هندسی بخش عمده دانشی بود که فلسفه و تعلیمات روشنفکرانه، به صورت مجزا، سعی داشتند به دانش آموزان و دانشجویان این رشته کاربرد آن را به اثبات برسانند.
دوم، این مکتوب به کمک شواهد غیرقابل انکار، به تثبیت و تشریح نیروی برتر منطق بشری و قابلیت آن برای استنباط و قاعده گذاری بر طبق قوانین سیستماتیک استدلالی میپرداخت.
سوم اینکه «اصول» به واسطه ادعای جامع خود به عنوان یک نمونه اصیل و عالی از منطق، سطح مطالعات ریاضی را از حالت صرفاً کاربردی آن به علوم زیباییشناسی ارتقاء داد.








































ver very good!tnx!