گام‌های هپتاتونیک؛ ساختار، نامگذاری و کدینگ (۲)

ساختار فاصله ای گام هپتاتونیک را می توان به صورت دایره با چرخش در جهت عقربه ساعت نیز نشان داد. به این شکل، ساختار دایره‌ای فواصل می گوییم:

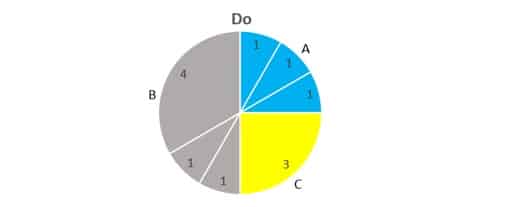
با بررسی ساختار فاصله‌ای گام‌های متعدد هپتاتونیک نتیجه می‌گیریم که جمع اندازه تمام فواصل تشکیل دهنده، معادل ۱۲ می باشد. بنابراین برای ساختن یک گام هپتاتونیک باید فواصل به گونه ای انتخاب شوند که:

• تعداد آنها هفت عدد باشد.
• جمع فواصل معادل ۱۲ باشد.

چگونه بر اساس ساختار فاصله ای، گام هپتاتونیک طراحی کنیم؟
یک ساختار فاصله‌ای در گام هپتاتونیک دو ماژور را می توان به این شکل نشان داد:

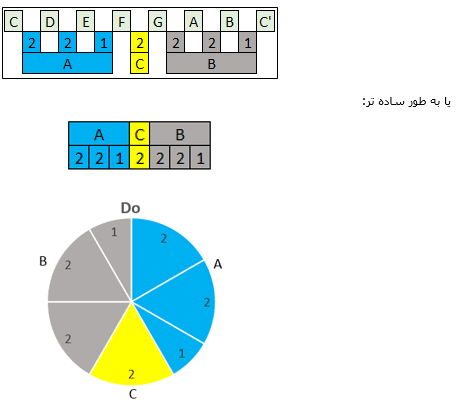
همانطور که در اشکال بالا مشخص است، ساختار فاصله‌ای به سه قسمت تقسیم می شود: یک بخش میانی به نام C و دو بخش A و B. بخش‌های A و B نیز هرکدام از سه قسمت تشکیل می‌شوند. اندازه بخش C می‌تواند بین ۱ و ۶ باشد:

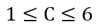
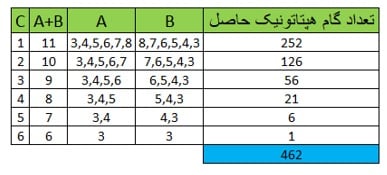
جمع کل اعداد مرتبط با این سه بخش نیز معادل ۱۲ است. با توجه به اندازه C، می توان اندازه بخش‌های A و B را مشخص کرد. به جدول زیر نگاه کنید:

طبق جدول بالا اگر اندازه بخش C برابر ۳ باشد، جمع A و B برابر ۹ خواهد شد. این بدان معناست که اگر اندازه A یکی از اعداد ۳,۴,۵ یا ۶ باشد، آنگاه اندازه بخش B یکی از اعداد ۶,۵,۴ یا ۳ خواهد شد.

حال با توجه به اینکه هر بخش A و B نیزهرکدام از سه قسمت تشکیل می شوند، باید اندازه این قسمت‌ها نیز مشخص شود. اگر A را معادل ۳ بگیریم، تنها یک حالت می‌توان فرض کرد تا جمع عدد فاصله سه قسمت آن برابر ۳ شود:

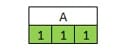
با فرض A=C=3، B نیز معادل ۶ خواهد شد:

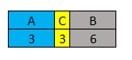
حال باید دید چند حالت می توان در نظر گرفت تا جمع اندازه فواصل سه قسمت B برابر ۶ شود:

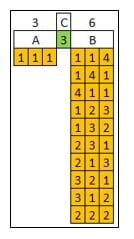
با توجه به شکل بالا برای قسمت B=6 می توان ۱۰ حالت مختلف در نظر گرفت که بعضا جایگشت‌های (Permutation) یکدیگرند. با فرض A=C=3 و B=6 و با اتصال A و C به انواع تقسیمات B ،۱۰ گام هپتاتونیک به دست آورد:

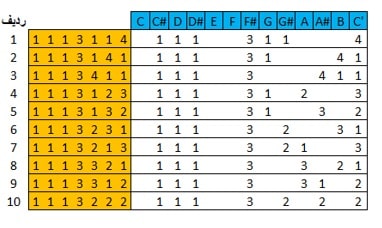
درشکل بالا عددی مانند ۳ گویای آن است که بین D# و F# یک فاصله سه نیم‌پرده‌ای وجود دارد. ساختار دایره‌ای گام‌های ردیف ۲,۱ و ۱۰ به شکل زیر هستند:

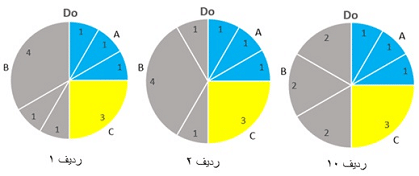
درنهایت و با درنظر گرفتن تمام حالات ممکن برای تمام مقادیر A,B وC، به عدد ۴۶۲ می رسیم. به این ترتیب می توان از یک گام دودکافونیک، ۴۶۲ گام هپتاتونیک مختلف ایجاد نمود:

در این لینک می توانید فایل اکسل شامل تمام ۴۶۲ ساختار فاصله ای را مشاهده کنید.