در سیستم ۵۰ قسمتی نیز دو اندازه متفاوت از سوم کوچک و بزرگ مشاهده می شود که بر اساس نوع انتخاب ما می توان سوم میانه میانگین را مشاهده نمود. مثلا اگر سوم کوچک ۲۸۸ سنت و سوم بزرگ ۳۸۴ سنت باشد، فاصله سوم میانه معادل ۳۳۶ سنت خواهد شد ولی اگر سوم کوچک ۳۱۲ سنت و سوم بزرگ ۳۸۴ سنت انتخاب شود، فاصله سوم میانه ۳۴۸ سنتی در سیستم وجود ندارد. به این ترتیب فرض هلمهولتز که سوم میانه یا خنثی را میانگین سوم کوچک و بزرگ فرض کرده در همه موارد صدق نمی کند.
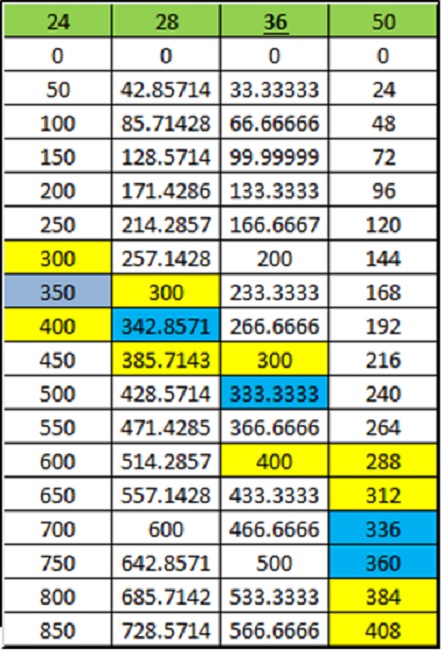
فواصل خنثی در سیستمهای شکل گرفته براساس چرخه فاصله پنجم
در سیستم هایی که بر اساس چرخه فاصله پنجم شکل می گیرند (مانند سیستم فیثاغورثی) فواصل خنثی یا میانه را می توان مشاهده نمود. در شکل زیر درجات ۱۹ تا ۲۲ چرخه بالارونده یا پایین رونده پنجم اندازه های متفاوتی برای فواصل دوم- سوم- ششم و هفتم میانه یا خنثی را بدست می دهند. مثلا درجه ۱۹ بالارونده در چرخه پنجم، فاصله دوم میانه ای معادل ۱۳۷.۱۴۵ است حال آنکه درجه ۲۲ پایین رونده اندازه دوم میانه را برابر با ۱۵۶.۹۹ سنت بدست می دهد:
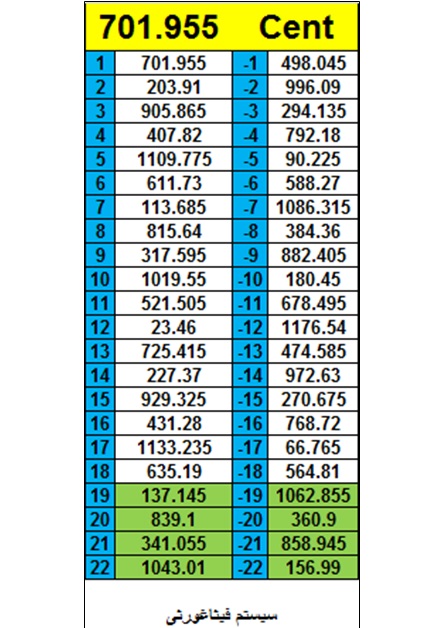
نیکالوس مرکاتور، ریاضیدان قرن ۱۷ آلمانی، در یک چرخه ۵۳ تایی فاصله پنجم ۲/۳ متوجه اختلافی معادل ۳.۶۱۵ سنت شد و آن را «کمای مرکاتور» نامید. (mercator 2017)
او با تعدیل فاصله پنجم به اندازه ۵۳/۱ کمای مرکاتور به گام ۵۳ قسمتی مساوی که شبیه سازی عالی است از سیستم فیثاغورثی دست یافت. (equal temperament 53:2017)
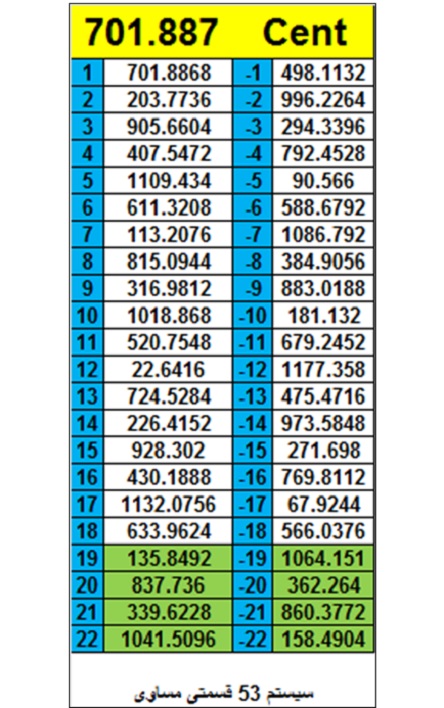
اختلاف اندازه های مختلف یک فاصله میانه در چرخه بالارونده و پایین رونده پنجم در سیستم ۵۳ قسمتی مساوی، معادل یک کمای هولدر یعنی ۲۲.۶۴۱۵ سنت است. (۲۰۱۷ Holdrian comma)
در سیستم ۵۳ قسمتی مساوی بعد از ۳۱ چرخه پنجم، دوم میانه دیگری معادل ۱۵۸.۴۹۷ سنت بدست می آید. حال آنکه در سیستم فیثاغورثی اندازه آن برابر با ۱۶۰.۶۰۵ سنت است.
فواصل خنثی در محدوده “N-Limit”
فواصل خنثی به صورت نسبتهای کسری نیز اندازه های متنوعی را شامل می شوند. در محدوده های “N-Limit” (مهاجری ۲۰۱۸) می توان مثالهای متنوعی از فواصل خنثی را ذکر کرد:
– محدوده “۳-Limit”: سیستم فیثاغورثی در محدوده “۳-Limit” بوده و قبلا ذکرگردید.
– محدوده “۵-Limit”: این محدوده براساس هارمونیک ۵ ام شکل گرفته وعدد ۳ را نیز شامل می شود. می توان از فاصله دوم میانه ۲۵/۲۷ با اندازه ۱۳۳.۲۳۸ سنت به عنوان یک فاصله خنثی در این محدوده یاد کرد. این فاصله توسط فارابی معرفی شده بود. (برکشلی ۱۲۵:۱۳۵۷)
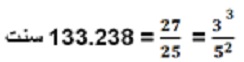
– محدوده “۷-Limit”: این محدوده براساس هارمونیک ۷ ام شکل گرفته وعدد ۳ و ۵ را نیز شامل می شود. می توان از فاصله دوم میانه ۳۲/۳۵ با اندازه ۱۵۵.۱۴ سنت به عنوان یک فاصله خنثی در این محدوده یاد کرد. این فاصله در واقع هارمونیک ۳۵ ام می باشد:
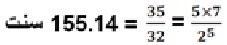
همچنین فاصله سوم میانه ۴۰/۴۹ با اندازه ۳۵۱.۳۳ سنت یک فاصله خنثی در این محدوده است:
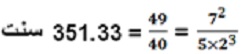
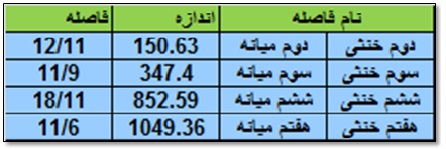
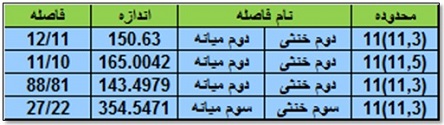
– محدوده “۱۱-Limit”: هارمونیک ۱۱ ام منشاء شکل گیری محدوده “۱۱-Limit” است. این محدوده اعداد ۳ و ۵ و۷ را نیز شامل می شود. در شکل زیر می توان درجات میانه براساس محدوده “۱۱-Limit” را مشاهده نمود. در شکل گیری این فواصل اعداد اول ۳ و ۱۱ نقش دارند:
دکتر برکشلی در کتاب «اندیشه های علمی فارابی درباره موسیقی» می نویسد که فارابی در معرفی ابعاد ملایم کوچک با نسبت:
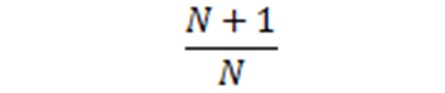
از نسبت هایی مانند ۱۱/۱۲ و ۱۰/۱۱ و یا فواصلی با تسبتهای متفاوت مانند ۲۲/۲۷ و ۸۱/۸۸ نام می برد. (برکشلی۱۲۵:۱۳۵۷):
با این حال سیاوش بیضایی در مقاله «سرچشمه ربع پرده در موسیقی ایران» معتقد است، اولین بار منصور زلزل فاصله ۱۱/۱۲ را معرفی نموده است.
(سیاوش بیضایی ۱۳۸۲)
– محدوده “۱۳-Limit”: هارمونیک ۱۳ ام منشاء شکل گیری محدوده “۱۳-Limit” است. این محدوده اعداد ۳ و ۵ و۷ و ۱۱ را نیز شامل می شود. فارابی و ابن سینا فواصلی از این محدوده را به عنوان فواصل خنثی معرفی کرده اند:
• فارابی با ارائه فاصله ای مانند ۱۲/۱۳ (برکشلی۱۲۵:۱۳۵۷):

• ابن سینا با ارائه فواصلی مانند ۱۳/۸ و ۳۲/۳۹ (۲۰۱۷ Schulter):

جالب است بدانیم که نسبت ۳۲/۳۹ همان هارمونیک ۳۲ ام است. بر اساس هارمونیک ۱۳ ام می توان چهار فاصله خنثی یا میانه دیگر را بدست آورد:
فاصله ۶۴/۱۱۷ نیز همان هارمونیک ۱۱۷ می باشد.
منابع
– بیضایی، سیاوش.۱۳۸۲. خاستگاه ربع پرده در موسیقی ایران. فصلنامه ماهور سال ششم شماره ۲۱
– برکشلی،مهدی. ۱۳۵۷. اندیشه های علمی فارابی درباره موسیقی.تهران: پژوهشگاه موسیقی شناسان ایران
–
مهاجری،شاهین. شبیه سازی فواصل گام ۲۴ قسمتی مساوی براساس هارمونیک یازدهم
(آخرین دسترسی ۲۶/۰۲/۲۰۱۸)
www.harmonytalk.com/id/18190
– Alves ,William.2013. Music of the Peoples of the World. Boston:Schirmer
– Skinner, Miles Leigh.2007. Toward a Quarter-tone Syntax: Analyses of Selected Works by Blackwood, Haba, Ives, and Wyschnegradsky.
(آخرین دسترسی ۱۹/۰۴/۲۰۱۷)
http://www.tierceron.com/diss/intro/intro.pdf
– Helmholtz , Hermann . 1885. On the Sensations of Tone as a Physiological Basis for the Theory of Music. London:
Longmans, Green.
(آخرین دسترسی ۱۹/۰۴/۲۰۱۷)
https://archive.org/details/onsensationsofto00helmrich
– Huygens-Fokker Foundation. List of intervals.
(آخرین دسترسی ۱۹/۰۴/۲۰۱۷)
http://www.huygens-fokker.org/docs/intervals.html
– Ghrab , Anas.2005. Occident and Intervals in “Arabic Music,” from the Seventeenth Century to the Arabic Music Congress. the world of music vol. 47(3)
(آخرین دسترسی ۱۹/۰۴/۲۰۱۷)
https://www.academia.edu/860399/The_Music_of_Others_in_the_Western_World
– Keenan,Dave.1999. A note on the naming of musical intervals.
(آخرین دسترسی ۱۹/۰۴/۲۰۱۷)
http://www.dkeenan.com/Music/IntervalNaming.htm
– Mercator’s comma٬
(آخرین دسترسی ۰۲/۰۵/۲۰۱۷)
http://tonalsoft.com/enc/m/mercator-comma.aspx
– ۵۳ equal temperament
(آخرین دسترسی ۰۲/۰۵/۲۰۱۷)
https://en.wikipedia.org/wiki/53_equal_temperament
– Holdrian comma
https://en.wikipedia.org/wiki/Holdrian_comma#Mercator.27s_comma_and_the_Holdrian_comma
(آخرین دسترسی ۰۲/۰۵/۲۰۱۷)
– Schulter , Margo.2014. Are there intervals in Eastern music using the eleventh harmonic, such as the neutral third 11/9
https://www.quora.com/Are-there-intervals-in-Eastern-music-using-the-eleventh-harmonic-such-as-the-neutral-third-11-9
(آخرین دسترسی ۱۹/۰۴/۲۰۱۷)



















با سپاس فراوان
سپاس