قبلا گفته شد می توان بین هارمونیک های دوم و چهارم و هشتم و شانزدهم و… سیستم اکتاوی تشکیل داد. حال در اینجا باید گفته شود که اصولا بین هارمونیکهای fm و fn به شرط fm=2fn می توان سیستم اکتاوی فواصل را مشاهده نمود. سیستم زیر فواصل بین هارمونیک های ۱۵ تا ۳۰ را نشان می دهد. در این سیستم fm=30 و fn=15 بوده و فواصل کسری ساده شده اند:
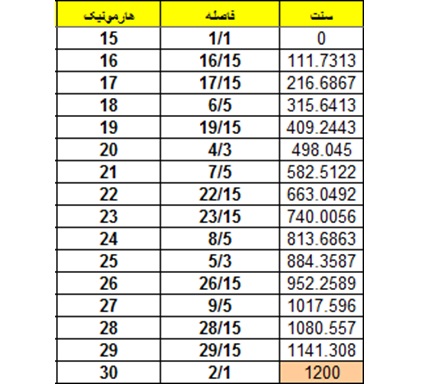
سری هارمونیک و سیستم فواصل “ARDO”
در بالا اشاره شد که در سری هارمونیک و بین هارمونیک های fm و fn به شرط fm=2fn سیستم اکتاوی شکل می گیرد. این سیستم اکتاوی را سیستم حسابی «تقسیمات کسری اکتاو» (Arithmetic rational divisions of octave) یا به صورت مخفف “ARDO” می نامیم. چون ماهیت این سیستم کسری است می توان از لغت “Rational” صرفنظر کرده و آن را “ADO” بنامیم (Arithmetic divisions of octave).
این سیستم، سیستم اکتاوی است که براساس تصاعد حسابی بین حاصل کسرهای فواصل شکل می گیرد. برای نامگذاری این سیستم از اولین هارمونیک موجود در سیستم فواصل انتخابی استفاده می کنیم. به این ترتیب عنوان کلی m-ADO گویای این است که سیستم از هارمونیک m ام شروع می شود. به عنوان مثال سیستم ۱۵-ADO سیستمی است از فواصل که هارمونیکهای ۱۵ تا ۳۰ را شامل شده و از هارمونیک ۱۵ شروع می شود.
به عدد ۱۵ یا هر هارمونیکی که سیستم با آن شروع شود اندازه یا کاردینالیتی (Cardinality) سیستم می گوییم. کاردینالیتی تعداد فواصل موجود در سیستم را مشخص می کند. در سیستم ۱۵-ADO کاردینالیتی و تعداد فواصل سیستم برابر ۱۵ است. فواصل این سیستم همگی نسبت به اولین هارمونیک سیستم (در اینجا هارمونیک ۱۵ ام) محاسبه می شوند:
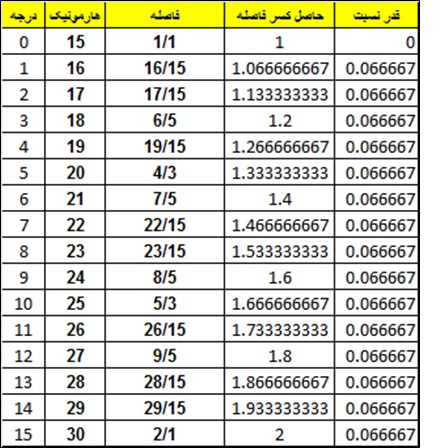
قبلا گفتیم که این سیستم بر اساس تصاعد حسابی بین حاصل کسرهای فواصل شکل می گیرد. در سیستم با کاردینالیتی m قدر نسبت تصاعد که با حرف d نمایش داده می شود برابر با ۱/m بوده و درجه a دارای حاصل کسری Ra معادل زیر است:
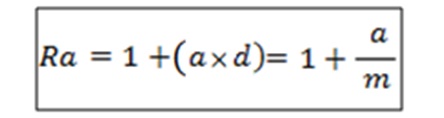
مثلا درجه ۱۱ ام در سیستم فواصل ۱۵-ADO دارای حاصل کسری برابر با ۱.۷۳۳۳۳ است:
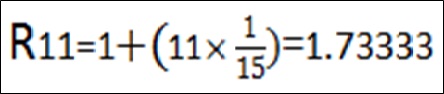
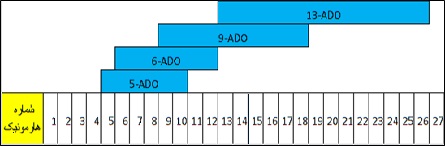
در شکل زیر ۴ سیستم فاصله ای را که بر اساس هارمونیک های ۵، ۶، ۹ و ۱۳ شکل گرفته اند می بینیم. در اینجا نکته ای قابل ذکر است که نمی توان هارمونیک fm را به گونه ای انتخاب کرد که عدد فرد باشد چرا که شرط fm=2fn برقرار نمی گردد. به عنوان مثال هارمونیک ۱۳ ام را نمی توان به عنوان هارمونیک fm انتخاب کرد چون fn=6.5 در سری هارمونیک وجود ندارد.
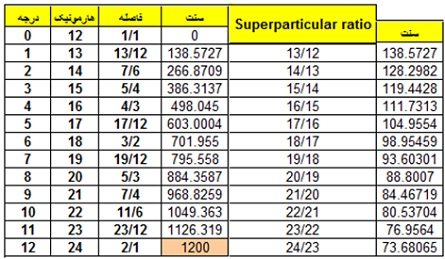
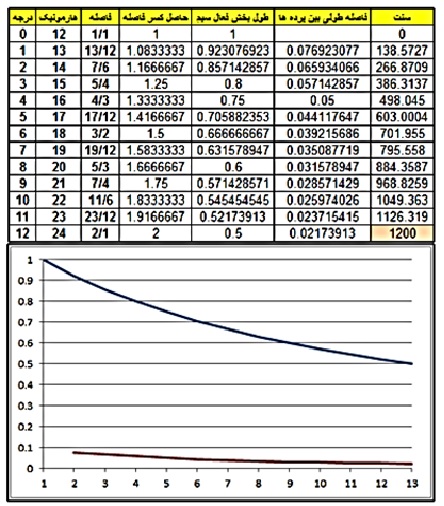
فاصله بین درجات متوالی در سیستم فواصل m-ADO همگی “Superparticular” هستند. در زیر اندازه فواصل بین درجات متوالی سیستم ۱۲-ADO را مشاهده می کنیم. قابل ذکر است که با افزایش درجه در سیستم اندازه فواصل بین درجات “Superparticular” کاهش می یابد:



















۱ نظر