درباره رابطه موسیقی، فیزیک و ریاضی بسیار مطلب می توان نوشت؛ بهترین نمود این ارتباط را می توان در ارتعاش و تولید صدا و شکل گیری فواصل موسیقایی و تنوع آنها پیدا کرد. تعریف فاصله موسیقی را همه ما می دانیم: رابطه ای ادراکی بین دو صوت که بر اساس تفاوت ارتفاع صدا شکل می گیرد. درک ما از ارتفاع صدا پدیده روانشناختی پیچیده ای است و ناشی از تاثیر فرکانس ارتعاش بر سیستم شنوایی و عصبی ما می باشد. اختلاف فرکانس اصوات منجر به اطلاق عناوینی مانند «زیر» و «بم» به صدا می گردد. در واقع فاصله موسیقایی ادراکی است که از تفاوت زیر و بمی دو صدای متوالی ایجاد می شود. طبیعی است دو صدای هم فرکانس نیز دارای فاصله موسیقایی باشند.

گفتیم منشاء هر صدایی ناشی از ارتعاش ماده ای است که ارتجاع پذیر بوده و دارای فرکانس ارتعاشی متناسب با یک سری فاکتورهای فیزیکی است. مثلا نوت A4 دارای فرکانس ۴۴۰ هرتز است، تا اینجا ما فقط یک صدا داریم و فاصله موسیقی معنایی ندارد. حال اگر صدای دومی را بعد از نوت A4 ایجاد کنیم که مثلا دارای فرکانس ۴۷۰ هرتز باشد، اختلاف بین زیر و بمی این دو صدای «متوالی» را به عنوان فاصله موسیقی درک می کنیم. پس فاصله موسیقایی وابسته به وجود دو صدا با فرکانسهای مساوی یا متفاوت است. فواصل موسیقی متنوع بوده و توالی آنها تاثیر روانشاختی متفاوتی ایجاد میکند. توالی فواصل موسیقایی منجر به شکل گیری یک سیستم صوتی می گردد که در شکل گیری ملودی نقش دارد. ملودی در این سیستم می تواند ساختار تونال، مدال یا آتونال داشته باشد.

سری هارمونیک
موقعی که جسمی ارتجاع پذیر به ارتعاش در می آید صدای حاصله دارای یک موج مرکب است که ترکیبی است از صداهایی با طول موج و فرکانس متفاوت (یا به عبارتی یک فرکانس اصلی و یک سری فرکانس های فرعی). با کمک فرمول های ریاضی سری فوریه (Fourier) می توان این موج مرکب را به اشکال ارتعاشی سازنده اش تجزیه کرد. اگر فرکانس صدای اصلی را f فرض کنیم فرکانس هارمونیک ها مضرب صحیحی از f می باشد:
فرکانس اصلی یا هارمونیک اول = f1
فرکانس هارمونیک دوم = ۲f1
فرکانس هارمونیک سوم = ۳f1
فرکانس هارمونیک چهارم = ۴f1

به این ترتیب هارمونیک nام دارای فرکانسی معادل nf1 می باشد. توالی این هارمونیکها «سری هارمونیک» را به وجود می آورد. از نظر ریاضی تعداد هارمونیکها در این سری نامتناهی بوده ولی به دلیل محدودیت های فیزیکی تعداد هارمونیکها محدود می باشند. هنگام ارتعاش جسم ارتجاع پذیر، اشکال ارتعاشی هارمونیک ها با هم ترکیب شده و موج نهایی ارتعاشی را می سازند:

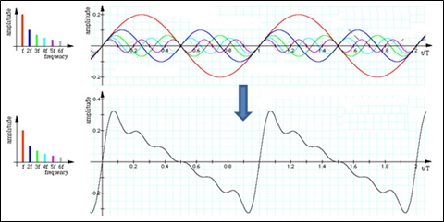
از نظر ریاضی، مضارب هارمونیک ها در بین خود رابطه ای ایجاد می کنند که نوعی «دنباله ریاضی» است. دنباله (sequence)، تابعی است که دامنه آن مجموعه اعداد طبیعی یا قطعه ای از مجموعه اعداد طبیعی باشد. از آنجایی که از نظر ریاضی تعداد هارمونیک ها نامتناهی هستند این دنباله نامتناهی بوده و چون جملات آن مثبت می باشد، دنباله ای صعودی است. برای مشخص کردن یک دنباله باید با یک ضابطه آن را مشخص کرد.

ضابطه یک دنباله را در اصطلاح «جمله عمومی آن دنباله» می‌گوییم. برای نمایش مقدار دنباله f به ازای عدد طبیعی از نماد (f(n یا معمولاً از نماد {fn} استفاده می کنیم. جمله عمومی مضارب سری هارمونیک به صورت زیر است:

از سوی دیگر سری هارمونیک نوعی «تصاعد حسابی» است. تصاعد حسابی “arithmetic progression” به دنباله‌ای از اعداد گفته می شود که اختلاف هر دو جمله متوالی آن مقداری ثابت، مثلاً d باشد. به عدد ثابت d قدر نسبت تصاعد گفته می شود. برای نمونه دنبالهٔ ۱، ۲، ۳، ۴، ۵، ۶ و … یک تصاعد حسابی از اعداد با قدر نسبت ۱ می باشد.

اگر جمله اول یک تصاعد حسابی a1 و قدر نسبت آن d باشد آنگاه جملهٔ i ام این تصاعد برابر خواهد بود با:

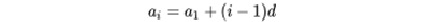
در سری هارمونیک اصوات با فرض a1=1 و d=1 ضریب هارمونیک ۱۲ برابر با ۱۲ خواهد بود:

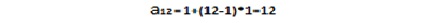
حال در این جا نگاهی به سری هارمونیک های نت C2 می اندازیم. به شکل زیر دقت کنید:

در شکل بالا ۱۶ هارمونیک ابتدایی نت C2 مشخص است. اعداد بالا و پایین نت ها نشان دهنده میزان اختلاف ارتفاع نت ها در سیستم ۱۲ قسمتی مساوی با ارتفاع هارمونیک متناظر خود است. مثلا ارتفاع هارمونیک ۱۱ از نت فا دیز معتدل ۴۹ سنت کمتر است و معادل فاسری است.

گفته شد که از نظر ریاضی تعداد هارمونیک ها نامحدود می باشد. بنابراین می توان تعداد جملات دنباله تصاعد حسابی را تا بی نهایت تصور کرد.