نمونه ای از ایده پردازی در موسیقی میکروتونال
چکیده
در این نوشتار نحوه استفاده از اشکال هندسی در موسیقی میکروتونال از طریق بیان چندین مثال مورد بررسی قرار گرفته است. هندسه علم بنیادین فرم ها و نظم موجود در آن هاست. هندسه و ریاضی از طریق تناسب و تقارن، ابزار معینی را برای کاربرد در موسیقی شکل داده اند. تناسبات درهندسه مورد تجزیه و تحلیل قرار گرفته و میتواند به عنوان جنبه اصلی زیبایی شناختی در موسیقی مطرح گردد. براساس نظریه فیثاغورس قواعدی کلی برای هارمونی و تناسبات وجود دارد.این قواعد در موسیقی نیز به کار گرفته شده اند.این اصول بر پایه علم هندسه استوار هستند. در این مقاله نمونه هایی در زمینه کاربرد هندسه و اشکال هندسی در طراحی توالی فواصل مورد بررسی قرار می گیرد و در نهایت مثال هایی شنیداری ارائه خواهد شد.
لغات کلیدی: میکروتونال، هندسه، چندضلعی، توالی فواصل، ایده پردازی
مقدمه
موسیقی میکروتونال بر پایه توالی فواصل به غیرازترکیبات نیم پرده ای شکل میگیرد. دراین نوع موسیقی، یک آهنگ ساز دردنیایی از فواصل و گامهای برآمده از سیستمهای مختلف غرق خواهد شد.او میتواند براساس مدلهای مرسوم و مفروض به طراحی توالی فواصل صوتی خود اقدام کرده یا منابع غیر موسیقایی را به عنوان ایده ای برای طراحی توالی فواصل صوتی خود در نطر بگیرد.
هندسه شاخه ای از ریاضی وعلم فرم ها و بررسی تناسب، تقارن و نظم موجود دراشکال است. در نقاشی و معماری، قواعد هندسی ابزار معینی را برای طراحی اشکال به دست داده اند. از طرفی تناسبات هندسی موجود در طبیعت نیز در طول تاریخ مورد بررسی قرار گرفته و به عنوان یکی از منابع اصلی هدایت زیبایی شناختی درهنر مطرح گردیده اند. این تناسبات می توانند به عنوان عاملی برای ایجاد هماهنگی و هارمونی در معماری و همچنین شاخه های مختلف هنر، از جمله موسیقی مد نظر قرار گیرند.
در دیدگاه فیثاغورس، تمام رویدادها تحت تاثیر اصولی کلی رخ می دهند که تابع قوانین ریاضی اند. حساب، هندسه، ستاره شناسی و موسیقی، علوم چهارگانه ای هستند که کاملا برمبنای قواعد کلی فوق الذکر شکل گرفته اند. فیثاغورس متقاعد شده بود که هارمونی و تمام موضوعات و اصول موجود در جهان هستی می تواند از طریق اعداد و قواعد ریاضی به خوبی درک شود. او کشف کرد که فواصل موجود میان نت های موسیقی ارتباطات ساده ای را بر اساس تقسیمات طولی در تارها و تعداد نوسانات شکل می دهند.
هندسه به عنوان مبنای ایده پردازی
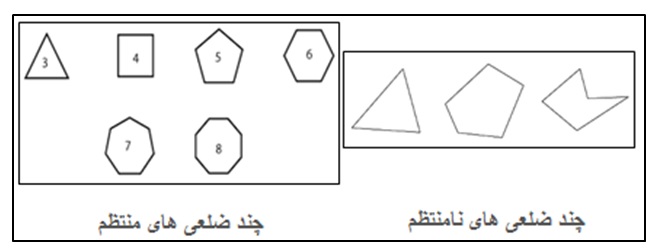
تناسبات موجود در اشکال هندسی، از جمله نسبتهای طولی، می توانند مبنایی برای ایده های موسیقایی باشند. از جمله این اشکال هندسی میتوان از چند ضلعی “Polygone” نام برد. چند ضلعی شکلی دو بعدی است که توسط تعداد نامتناهی خطوط راست به نام ضلع محدود شده است. به جمع طول این اضلاع محیط چند ضلعی گویند. چند ضلعی ها گاهی دارای اضلاع و زوایای مساوی هستند که به آنها چند ضلعی منتظم گویند و گاهی به دلیل نامساوی بودن تعداد اضلاع یا زاویه ها، نامنتظم می باشند:
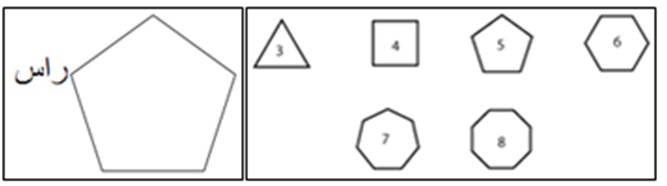
به محل تقاطع دو ضلع، راس چند ضلعی گویند. تعداد رئوس و اضلاع درچند ضلعی ها برابر است. نامگذاری چند ضلعی ها براساس تعداد اضلاع و رئوس آن صورت می گیرد. از جمله چند ضلعی ها می توان به سه ضلعی، چهارضلعی، پنج ضلعی، شش ضلعی و… اشاره کرد:


















۱ نظر