مندلبرت، پدر هندسه ی فراکتالی، فراکتال را بدین صورت تعریف میکند: “یک شکل فراکتالی مجموعه ای از اشکال در هم پیچیده و مجزاست بطوریکه اگر یک قطعه از آن را بزرگ کنیم، شکل حاصل همانند شکل نخستین در خواهد آمد و همچنین با احتمالی اندک بدشکل و بیریخت خواهد شد”
اساس ساخت فراکتال همان چیزی است که در ریاضی به آن تکرار میگوییم. هر گاه روی یک معادله غیرخطی تکرارپذیری صورت گیرد میتوان به یک شکل فراکتالی رسید. الگوریتم این کار به این صورت خواهد بود:
۱- یک ورودی (x) را به تابع بدهید.
۲- جواب تابع را برحسب ورودی داده شده به آن حساب کنید
(f(x) =y1)
3- جواب بدست آمده از مرحله قبل (y1) را مجددآ به عنوان یک ورودی جدید درون همان تابع جایگزین کنید
(y2=f(y1))
4- برای بدست آوردن مقادیر بعدی، مرحله سوم را به ازای اندیس های بعدی، تکرار کنید.
تا بدین جا توانستیم بصورت خیلی ساده برای فراکتالی که به روش تکرار روی تابع دلخواه (f) تولید میشود، مقادیر خروجی را بدست آوریم. حال اگر قرار باشد این فراکتال را روی صفحه نمایش در یک کامپیوتر داشته باشیم، باید بین خروجی های عددی و پیکسل های صفحه نمایش، یک تناظر (نگاشت) ایجاد نماییم. در نهایت بسته به دقتی که روی مقادیر ورودی داشته ایم، شکلی دقیقتر بدست خواهیم آورد؛ در واقع هرچه مقادیر داده شده به تابع در دقتهای کوچکتری باشند، شکل نهایی نیز دقتی بالاتر خواهد داشت.
فراکتالها اشکال هندسی عجیبی هستند که قوانین هندسه اقلیدسی را در هم میشکنند و نمیتوان برای توصیف آنها از هندسه اقلیدسی کمک گرفت. در هندسه اقلیدسی اکثر اشکال مثل دوایر، مثلثها، مربع ها و دیگر چند ضلعی ها دارای محیط و مساحتی مشخص و قابل محاسبه هستند و چنانچه به آنها بنگرید، محیط آنها را یک خط یا منحنی میبینید؛ در صورتی که در فراکتال ها چنین نیست.
فراکتالها دارای محیط و مساحتی نامتناهی هستند. زیرا هر چه بیشتر روی محیط یک فراکتال دقت کنید، مقدار بیشتری برآمدگی و منحنی و ناهمواری ها و شکست ها و پیچش های مختلف را در آنها مشاهده میکنید که با وجود این ناهمواری ها و منحنی های بیشمار، محاسبه یک فاصله از دو نقطه روی فراکتال غیرممکن و امری محال است.
از آنجایی که اشکال فراکتالی نامتناهی هستند لذا ترسیم یک فراکتال بصورت کامل و با تمام جزئیات امکان پذیر نمیباشد. باید اضافه کرد که با وجود اینکه نمیتوان شکل دقیقی از یک فراکتال کشید ولی همه ما میتوانیم فراکتال را بصورت تقریبی رسم کنیم. تقریب استفاده شده در یک شکل فراکتالی به عمق فراکتال برمیگردد و در عمق بیشتر، تصویر فراکتالی تقریب زده شده به شکل واقعی نزدیکتر خواهد شد.
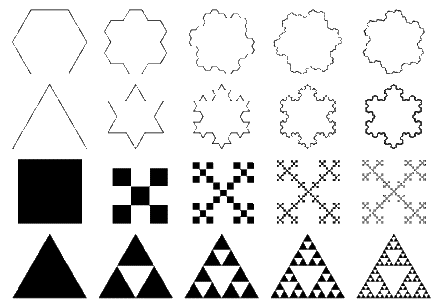
انواع اشکال فراکتالی را میتوان در دو دسته کلی جا داد:
• فراکتالهای خودتکرار کننده (self-repeating) که از فرمول های تکرارشونده ساده ای استفاده کرده و اشکالی ساده، مانند برف دانه کخ ( Koch snowflake) و مثلث سرپینسکی (Sierpinski triangle) خواهند داشت. از این گروه میتوان به فراکتالهای تئوری IFS و فراکتال های سیستمهای L
یا(L-systems) وGraftals و همانند اینها اشاره کرد.
• فراکتالهای خود متشابه (self-similar) که از نمای کلی شبیه به خود تکرار کننده ها هستند ولی در واقع اجزایی متفاوت از شکل کلی خود دارند؛ همانند مجموعه مندلبورت (Mandelbrot set)
موسیقی فراکتالی
با استفاده از فراکتالها به طرق مختلف میتوان به آهنگسازی و صدا سازی پرداخته و یا حتی از آنها ایده هایی جدید برای یک اثر هنری گرفت. راز نهفته در یک موسیقی فراکتالی همان چیزی است که در ریاضیات به آن نگاشت (map) میگویند.
نگاشت به این معنی است که یک ارتباط مستقیم و متناظر بین خروجی های عددی ( که از معادله حاصل میشوند) و پارامترهای خاصی (که برای ساخت آهنگ بکار میروند)، ایجاد کنیم. همانطور که برای تصویر کردن یک عکس فراکتالی، خروجی های تابع را به پیکسل های صفحه نمایش نگاشت میکردیم، حال باید پارامترهای ساخت آهنگ را به آن خروجی ها نگاشت کنیم.
پارامترهای ساخت آهنگ فراکتالی میتوانند شامل فرکانسها، اوزان، دینامیک و دیگر موارد در آهنگسازی باشند. از آنجا که پارامترهایی که در یک موسیقی فراکتالی بکار میروند بیشتر از یک عکس فراکتالی هستند، میتوان انتظار آهنگهایی متنوع تر نسبت به یک عکس فراکتالی را از یک فرمول واحد داشت. در مقاله بعد بیشتر به این موضوع پرداخته و همچنین نرم افزارهای آهنگسازی با استفاده از فراکتال ها را معرفی خواهیم کرد.
منابع:
Music From Fractal Noise – Michael Bulmer
Fractal Music,Hypercards and More… Mathematical Recreation from Scientific American Magazine – Martin Gardner
Fractal Music – Michael Carter
www.sciencedirect.com
www.emusician.com
www.tursiops.cc
www. java.sun.com
www. mathworld.wolfram.com
















masahate fraktala mahdoode
محیط فراکتال ها به بینهایت میل می کنه. فکر کنم منظور خانم شیدایی فر محیط بود و نه مساحت!
سلام ،
ممنون از لطف و توجه شما ،
باید بگم که مطالبی که خوندید رو با اسم منابع براتون گذاشتم تا در مورد صحیح بودن مطالب هم براتون شبهه بوجود نیاد اما برای بازتر شدن موضوع و توجیه اون اجازه بدین بررسی کنیم :
در اغلب موارد حرف شما دوست عزیز درست هست و مساحت یک فراکتال رو حتی با یه تقریبی هم میشه تخمین زد ؛ اما همیشه هم مساحت یک فراکتال محدود نیست!یه مثال ساده برای این موضوع اینه که اگه شما فراکتالی داشته باشین که در هر مرحله مساحتش یک n ام بشه،در نهایت مجموع شکل فراکتالی شما مساحتش بینهایت خواهد شد
(seriesSum(1/n, n, 1, infinity))=infinity
این طور:
۱+((۱)/(۲)) +( ((۱)/(۳)) +((۱)/(۴)))+( ((۱)/(۵))+((۱)/(۶))+ ((۱)/(۷))+ ((۱)/(۸ )))+ …>1+((1)/(2))+ (((1)/(4))+((1)/(4)))+(((1)/(8))+((1)/(8))+((1)/(8))+((1)/(8)))+…=۱+((۱)/(۲))+((۱)/(۲))+((۱)/(۲))+…=∞
مرسی!
(اگه مشکل خوندن فرمول تو اینجا هست ،کپی کنید تو یه صفحه چپ چین درست میشه)
بازم سلام وباز هم ممنون از این حوصله شما
بنده با حرف شما کاملا موافقم و هیچ ابهامی در این موضوع نمیبینم ولی منظور این بود که نامحدود بودن مساحت همیشگی نیست .که از مطالب بالا این قطعیت بر می آمد.
باز هم خسته نباشید
سلام خسته نباشید.واقعا ممنونم به خاطر مقالاتتون.من دانشجوی سال آخرمعماریم و سایت شما خیلی کمک کرد,امکانش هست مطالبی درباره رابطه موسیقی با کالبد بزارید؟
مثل فرم هارمونی ریتم نسبت هایی که درموسیقی کلاسیک کشف شده…
وجه تشابهی درموسیقی و معماری هست؟
بی زمانی موسیقی رو چطور میشه به ابدیت۱کالبدتبدیل کرد؟
منتظر جوابتون هستم!ممنون.
باید ذکر کنم من پایان نامم درباره موسیقی و معماری هست وممکنه نظراتتون رو رسالم تاثیر بزاره که مطمئنا اینطور خواهدبود.ممنون.
خانم یا آقای Monamo،
لطفا با ایمیل من (aviehs@yahoo.com) تماس بگیرید تا بتوانم در مورد پایان نامه تان به شما کمک کنم.
ba salam matlabe jalebi bod be lahaze akademiki mitone besyar komak kone
باسلام مطالب وبلاگ خوبه اما حجم مطالب کم است
سلام برای شرکت درریاضی پژوهان به مطالب بیشتری درمورد فراکتال نیازدارم
به زودی کتابی با نام “الفبای فراکتال” به بازار می آید. این کتاب از سطحی بسیار مقدماتی تا سطوح پیشرفته چگونگی ساخت انواع فراکتال را تشریح می کند…….
ایا شما کتابی در رابطه با فراکتال ها می شناسید؟
«لطفا راهنمایی کنید.»