موسیقی پنهان در اشکال منتظم هندسی
گفته شد که نسبت طولی، می تواند مبنایی برای ایده های موسیقایی باشد. اما چگونه؟ نسبت های طولی رابطه مستقیمی با اندازه فواصل موسیقایی دارند. فرض کنیم پنج ضلعی زیر را از یک راس باز کرده و به خط مستقیمی تبدیل کنیم:
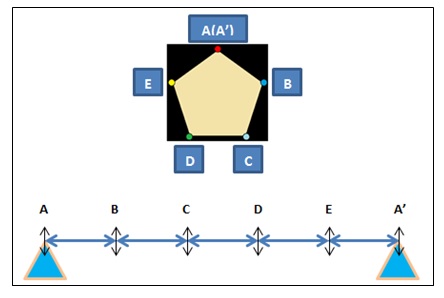
بعد از باز شدن چند ضلعی، می توان چنین تصور کرد که خط حاصله، یک سیم مرتعش بوده که مانند مونوکورد بر روی ۲ خرک قرار گرفته ورئوس آن جایگاه فواصل موسیقی است.
از آنجائیکه چند ضلعی مورد نظر منتظم است پس طول اضلاع، یا به عبارتی طول بین فواصل در روی سیم مرتعش مساوی می باشند. طول اضلاع را L می نامیم. به این ترتیب طول سیم معادل 5L می شود. با توجه به انطباق رئوس و محل قرار گیری فواصل موسیقی می توان طول بخشهای فعال مرتبط با هر فاصله موسیقی را به صورت زیر محاسبه کرد:
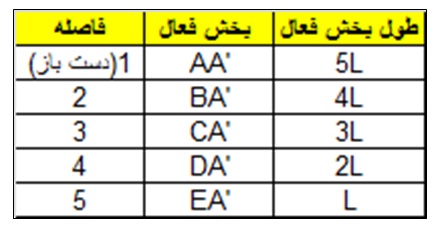
فواصل حاصله با توجه به مساوی بودن تعداد تقسیمات طولی سیم منطبق برسیستم فواصل تقسیم مساوی طول (۵-EDL) می باشند. به این ترتیب، فواصل موسیقایی عبارتند از:
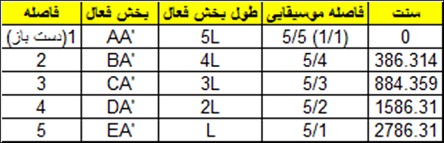
با گسترش این پنج فاصله به تعدادی از نوتهای بالاتر و پایین تر می توان به «توالی فواصل» زیر رسید:

 در اینجا، یک نمونه ملودی بر اساس این توالی صوتی را می توان شنید
در اینجا، یک نمونه ملودی بر اساس این توالی صوتی را می توان شنید
آنچه در بالا ارائه شده با این فرض بود که جمع طول اضلاع پنج ضلعی (یا محیط آن) معادل طول سیم مرتعش باشد. حال می توان به جای طول سیم مرتعش، طول اکتاو را معادل محیط پنج ضلعی باز شده در نظر گرفت. به این ترتیب سیستم فواصل ما به جای ۵-EDL، به ۱۰-EDL تبدیل خواهد شد و طول سیم مرتعش معادل محیط یک ۱۰ ضلعی منتظم بوده و به ۱۰ قسمت مساوی طولی تقسیم می شود:
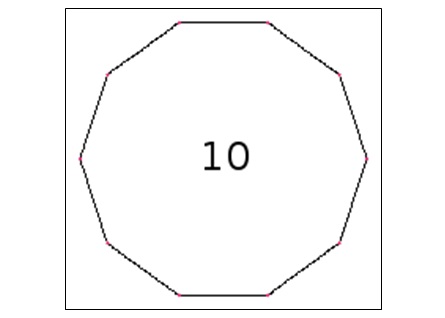
طول مربوط به فاصله اکتاو (یعنی نصف طول سیم مرتعش) در سیستم ۱۰-EDL به پنج قسمت مساوی تقسیم شده و محیط پنج ضلعی، طول نیمی از سیم (طول اکتاو سیم) را تحت پوشش قرار می دهد. تنها تفاوت در این است که در سیستم ۵-EDL اکتاوی وجود نداشته، اما در سیستم ۱۰-EDL اکتاو منطبق بر راس A’ خواهد شد:
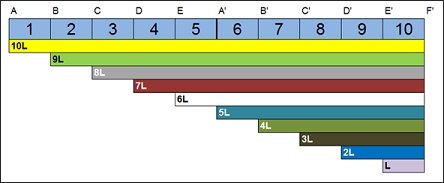
فواصل موسیقی دراین حالت عبارتند از:
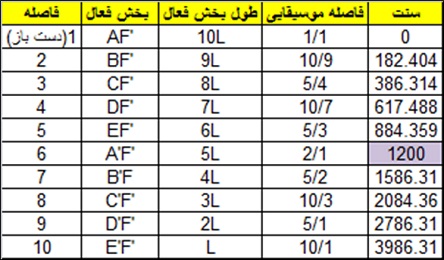
باید توجه داشت، فاصله اکتاو در سیستم هایی که براساس چند ضلعی هایی با تعداد اضلاع فرد شکل می گیرند وجود نداشته ولی می توان آنها را در قالب چند ضلعی های با تعداد اضلاع دو برابر گنجاند:
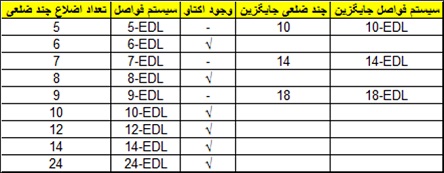
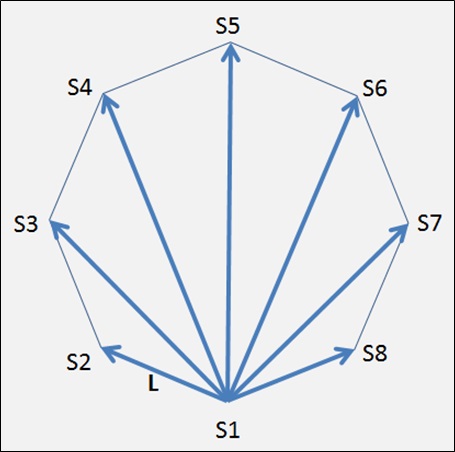
روش دیگر، کاربرد چند ضلعی های منتظم استفاده از خطوط واصل یک راس به سایر رئوس است. به مثال زیر نگاه کنید. شکل زیر یک هشت وجهی است با طول ضلع L که اقطار آن نیز مشخص است:
















۱ نظر