چکیده
گام ۲۴ قسمتی مساوی گام پیشنهادی استاد وزیری برای موسیقی دستگاهی از ابتدا با بازخوردهای متفاوتی روبرو شد. با اینحال از همان ابتدا این گام مبنای تئوری موسیقی ایرانی قرار گرفته است. با توجه به اندازه هارمونیک ۱۱ ام و معادل بودن آن با یکی از درجات گام ۲۴ قسمتی مساوی در این نوشته سعی شده است حداقل به صورت نظری معادلی غیرمعتدل برای این گام با دقت بالا و براساس ساختار هارمونیک ارائه شود.
مقدمه
گام ۲۴ قسمتی مساوی یا ۲۴-EDO گامی است از دسته گامهای معتدل مساوی که از ۲۴ فاصله مساوی ربع پرده ای تشکیل شده است. سابقه تاریخی کاربرد ربع پرده به یونان باستان برمی گردد. بعضی از تئوریسین های یونان مانند فیلولائوس (Irby 2016:168) و آریستوکسنوس
(Chalmers 1993:49)
فاصله ای معادل ربع پرده را در ساختار دانگ به کار بردند.
این گام در خاورمیانه و در قرن ۱۸ میلادی پی ریزی (Scott 1993)و تئوریسین هایی مانند میخائیل مشاقه در اوائل قرن ۱۹ میلادی آن را مفید دانستند (فرهت ۱۱۵:۱۳۷۸)
در ایران نیز استاد علینقی وزیری با نگاهی اعتدالی به فواصل موسیقی ایران کاربرد گام ۲۴ ربع پرده ای مساوی را پیشنهاد نمود. با این حال از سوی موزیسین های ایرانی موضع گیری هایی نسبت به این پیشنهاد انجام شده است.
چنانکه مهدی برکشلی بر عدم تایید این گام و عدم انطباق آن با روح موسیقی شرق تاکید داشته (دورینگ ۱۳۸۳: ۱۴۷) و از طرفی هرمز فرهت (فرهت ۱۱۸:۱۳۷۸) گام ۲۴ قسمتی مساوی را اختراع مصنوعی دانسته که مناسبتی با موسیقی ایران ندارد.
پاره ای دیگر از مخالفان این نظر معتقدند وزیری در حقیقت مادهای کاذب از نزد خویش ـ متأثر از مفروضات غربی ـ برای موسیقی سنتی فرض کرده و سپس تعدیلش کرده بود. (ممدپور ۱۳۸۴)
این گام بر اساس تقسیم لگاریتمی اکتاو به ۲۴ قسمت مساوی ایجاد می شود. در واقع هر نیم پرده گام ۱۲ قسمتی مساوی را به دونیمه مساوی تقسیم می کنیم:
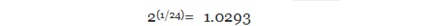

علامات و نامگذاری درجات ربع پرده ای
نگاهی به ساختارهارمونیک صدا
وقتی جسمی با فرکانسی خاص به صدا در می آید، علاوه بر فرکانس اصلی، فرکانس های فرعی دیگری نیز به وجود می آیند؛ اما چون شدت آن ها کم است، با گوش انسان شنیده نمی شوند. این فرکانس های فرعی نسبت خاصی با فرکانس اصلی دارند.
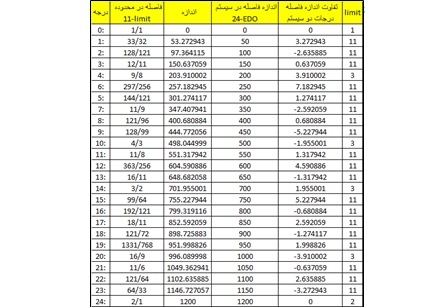
اگر نت DO زیر حامل کلید فا را به صدا در آوریم نتهای اصلی و فرعی ایجاد شده و اختلاف آنها با فواصل معتدل متناظر بر حسب سِنت (Cent) عبارت خواهند بود از:

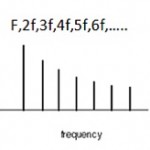
در حقیقت فرکانسهای فرعی همگی مضربی از فرکانس اصلی هستند (f، 2f، 3f،…) که ضرایب آنها در شکل آورده شده است. در اینجا فقط ۲۰ هارمونیک اول نشان داده شده است. بعضی از هارمونیکها در بعضی سازها و با گذر زمان تغییرات یا شدت کمتری دارند یا اصلاً تولید نمی شوند. همین عامل است که تفاوت بین سازها را تعیین می کند؛ به عبارت دیگر رنگ یا طنین ساز به وجود این اصوات بستگی دارد.
آنچانکه در شکل بالا مشخص است هارمونیکهای ۵ – ۷ – ۱۰ – ۱۱ – ۱۳ – ۱۴ – ۱۵ – ۱۷ و ۲۰ با فواصل معتدل اختلاف زیادی دارند. در این بین هارمونیک ۱۱ام با ندازه ۴۹- تقریب عالی از فاصله ربع پرده ای فا سری است است:
~ فا سری Fa#-49 = 551Cent
به این ترتیب می توان ردی از فواصل ربع پرده ای را در ساختار هارمونیک صدا پیدا نمود. اگر به هارمونیکها نظر دقیق تری بیاندازیم متوجه میشویم که هر هارمونیکی با یک عدد مشخص می شود:
– هارمونیک دوم با عدد ۲
– هارمونیک سوم با عدد ۳
– هارمونیک پنجم با عدد ۵
– هارمونیک هفت ام با عدد ۷
هری پارچ (Harry Partch) آهنگساز و تئوریسین آمریکایی (۱۹۷۴-۱۹۰۱) از این مشخصه استفاده کرد واعلام کرد میتوان مرزهای هارمونی را در سیستمهای فواصل گسترش داد
(Wolf 2003:13).
سیستم فیثاغورثی که از قدیم پایه ای برای اندازه گیری فواصل بوده است درواقع بر اساس چرخه فاصله پنجم یا همان هارمونیک سوم با نسبت ۳/۲ شکل گرفته است. بنابراین فواصل موجود در این سیستم مانند ۳/۲… ۹/۸… ۸۱/۶۴… ۲۷/۱۶ مضارب هارمونیکهای ۳ و ۲ هستند.
وی برای تبین مرزهای هارمونی در سیستم فواصل از لغت لیمیت (Limit) استفاده کرد. به این ترتیب می توان فواصلی که در سیستم فیثاغورثی می گنجند را به صورت ۳-Limit نمایش داد.
از طرفی اعداد اول در این بین اهمیت دارند چرا که اعداد فرد در واقع مضارب اعداد اول بوده و اعداد زوج هم نشان دهنده اکتاوهای یک هارمونیک می باشند.
هرچه عدد اول مربوط لیمیت افزایش یابد در واقع هارمونی ساختاری پیچیده تر پیدا می کند.
“n-limit” محدوده ای است که دربرگیرنده فواصل ناشی از هارمونیکهایی با عدد اول n و کمتر است
(Loy 2006:60).
به این ترتیب فواصل محدوده “۵-limit” شامل ترکیبات فاصله ای از هارمونیکهای ۳ و ۵ است. مانند: ۳/۲… ۵/۴… ۱۵/۸… ۴۵/۳۲
هر فاصله موسیقایی قابل تجزیه به مضارب اعداد اول است به صورت زیر:
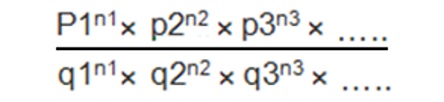
p و q اعداد اول بوده و n توان عدد اول است. فاصله ۹/۸ که حاصل دوبار چرخه فاصله ۳/۲ است در محدوده “۳-limit” به صورت زیر نمایش داده می شود:

فاصله ۲۵/۱۶ یا هارمونیک ۲۵ ام در محدوده “۵-limit” به صورت زیر نمایش داده می شود:

به مثالهای زیر دقت نمایید:

به این ترتیب تمام فواصل چه طبیعی و چه غیرطبیعی (مثلا ناشی ازتقسیمات مساوی اکتاو) را می توان به نوعی به ساختار هارمونیک صدا مرتبط کرد. البته در مورد فواصل سیستمهای تقسیم مساوی میتوان شبیه سازی را در لیمیت های متفاوت انجام داد. مثلا در مورد فاصله ۸۴۰ سنتی از سیستم ۳۰ قسمتی مساوی شبیه سازی های زیر انجام می شود:

حال که اندکی با مفهوم لیمیت و شبیه سازی فواصل غیرطبیعی در ساختار هارمونیک آشنا شدیم می توان به بررسی شبیه سازی فواصل ربع پرده ای پرداخت.
شبیه سازی گام “۲۴-EDO” بر اساس “۱۱-limit”
هچنانکه ذکر شد هارمونیک ۱۱ام با اندازه ۵۵۱.۳۱۷۹ سنت به عنوان شبیه سازی خیلی خوبی برای فاصله معادل فاسری ۵۵۰ سنتی مطرح می باشد. این فاصله در “۱۱-limit” قرار دارد. برای مشاهده فواصل موجود در لیمیت های مختلف می توان از جداول مختلف (List of pitch intervals) که در فضای مجازی موجود است استفاده کرد.
با این حال براساس ترکیب با فواصل دوم بزرگ فیثاغورثی (هارمونیک ۹ که در “۳-limit” قراردارد) و چهارم و پنجم درست٬ سایر فواصل نیز به دست می آیند. اولین فاصله ای که می توان به دست آورد اندازه یک ربع پرده در “۱۱-limit” است:
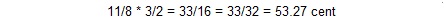
و فاصله سه ربع پرده ای “۱۱-limit”:
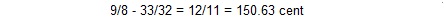
به این ترتیب می توان از ترکیب فواصل “۳-limit” و هارمونیک یازدهم مابقی فواصل را نیز پیدا نمود:
بحث
اختلاف اندازه فواصل سیستم میکروتونال ۲۴ قسمتی که در “۱۱-limit” طراحی شده است با سیستم ۲۴-EDOبسیار کم بوده و منطبق بر “JND=5…۸ cent10” است
:(AcousticsLab 2017)

JND یا “just noticeable difference” در مباحث سایکوآکوستیک “حداقل تفاوت ملموس” می باشد. همانطور که از نام این پارامتر پیداست، وظیفه اش نمایش میزان قابلیت انسان در تمیز دادنِ دو صدای مختلف است. این قابلیت در فرکانسها و شدت های مختلف، متفاوت است.
با آنالیز سیستم فواصل ارائه شده توسط نرم افزار “scalaver 2.36g11” موارد زیر مشخص می شود
(Scala 2017)
:
– سیستم فواصل از توالی دو اندازه ربع پرده تشکیل شده است:
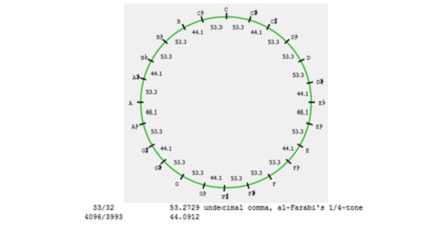
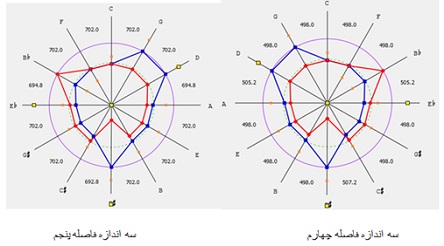
– سیستم از توالی سه اندازه فاصله پنجم و فاصله چهارم نا مساوی تشکیل شده است:
در مورد فواصل دیگر نیز چنین ترتیبی برقراراست. به عنوان مثال در مورد سوم خنثی:
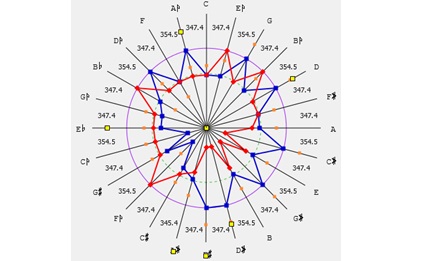
وجود اندازه های مختلف از یک فاصله بین درجات گام از جمله خصلتهای سیستمهای غیر معتدل است اما نکته مهم آن است که این اندازه ها بتوانند حس موسیقایی آن فاصله را ایجاد کنند. مثلا در مورد فاصله پنجم های متفاوت این سیستم که اندازه های حدود ۷۰۲.. ۶۹۴ و ۶۹۲ سنت را شامل میشوند می توان گفت با توجه به اندازه فاصله پنجم در سیستمهای مختلف کوک این شبیه سازی تقریب های خوبی را به دست می دهد:
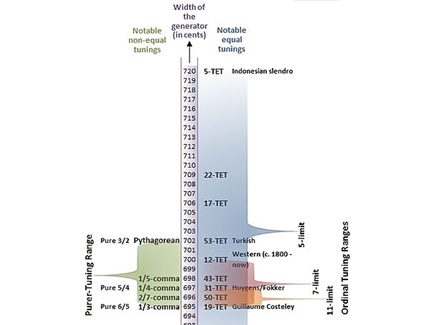
اندازه فاصله پنجم در سیستمهای مختلف کوک (برداشت از اینجا)
تفاوت اندک اندازه فواصل سیستم میکروتونال ۲۴ قسمتی که در “۱۱-limit” طراحی شده است با سیستم “۲۴-EDO” و همچنین تفاوت نامحسوس در اندازه فواصل چهارم و پنجم موجود در این سیستم گویای این است که سیستم ۲۴ قسمتی مساوی یا همان سیستم وزیری ( که در برگیرنده سیستم ۱۲ نیم پرده مساوی یا “۱۲-EDO” نیز هست) شبیه سازی خوبی است از فواصل بر اساس هارمونیک ۱۱ ام.
به عبارتی دیگر به خوبی میتوان بر اساس هارمونیک ۱۱ ام و “۱۱-limit” سیستمی غیر معتدل طراحی کرد تا مدلی باشد در کنار مدل های دیگر برای اجرای موسیقی دستگاهی. از طرفی لازم است در بررسی های بعدی به نقش هارمونیک های بالاتر مانند ۱۳ و ۱۷ و ۱۹ در این گونه معادل سازی ها پرداخت.
پی نوشت
مددپور، محمد، ۱۳۸۴٫ غربزدگی در موسیقی سنتی ایران، مقام موسیقایی شماره ۲۲، خرداد.
فرهت، هرمز .۱۳۷۸. مقوله دستگاه در موسیقی ایران. در سومین کتاب سال شیدا، گردآورنده محمدرضا لطفی، ۹۹ ۱۴۳. تهران: کتاب خورشید.
دورینگ، ژان. سنت و تحول در موسیقی ایرانی . ترجمه سودابه فضائلی . ۱۳۸۳ . تهران: انتشارات توس.
Georgia L . 2016. A Companion to Science, Technology, and Medicine in Ancient Greece and Rome , Volume 2.UK: John Wiley & Sons.
Chalmers, John H. Jr. 1993. Divisions of the Tetrachord. Hanover, NH: Frog Peak Music
Marcus,Scott .1993.The Interface between Theory and Practice: Intonation in Arab Music. Asian Music 24(2) :3958
Wolf, Daniel James.2003.Alternative Tunings, Alternative Tonalities.Contemporary Music Review 22 (1/2): 13
Loy,Gareth .2006 . Musimathics.London:Massachusetts: MIT Press.
AcousticsLab.2017.psychoacoustics. Perceptual attributes of acoustic waves – Pitch. http://acousticslab.org/psychoacoustics/PMFiles/Module05.htm(accessed Feb 10,2017).
HuygensFokker Foundation centre for microtonal music.2017.Scala Home page. http://www.huygensfokker.org/scala/ (accessed Feb 10,2017).








































ممنون از طرح موضوع.
برایم مشخص نشد چرا از هارمونیک ۱۱ استفاده کردید و چرا روی فاصله ۵۰ سنت یا ربع پرده و یا تقسیم ۲۴ تایی اکتاو تاکید دارید. تعیین فاصله ۱۵۰ سنتی (سه ربع پرده) برای فاصله «مجنب» برای مثال از سل تا لا کرن در شور سل به واقع این فاصله را از ماهیت خود خارج می کند.