همچنانکه در بخش پایین شکل بالا مشاهده می کنیم اولین درجه گام دارای طول بخش فعالی معادل طول سیم (با ضریب ۱) بوده و در واقع همان سیم دست باز است و طول بخش فعال درجه مربوط به فاصله اکتاو معادل نصف طول سیم (با ضریب ۰.۵) است. نمودار حاصل از طول بخش فعال سیم و فاصله طولی بین پرده ها نشان دهنده رابطه ای غیر خطی بوده و و فاصله طولی بین پرده ها همگی به یک اندازه نمی باشد.
جانی راینهارد (Johnny Reinhard) آهنگساز و نوازنده فاگوت، از جمله کسانی است که در سیستم
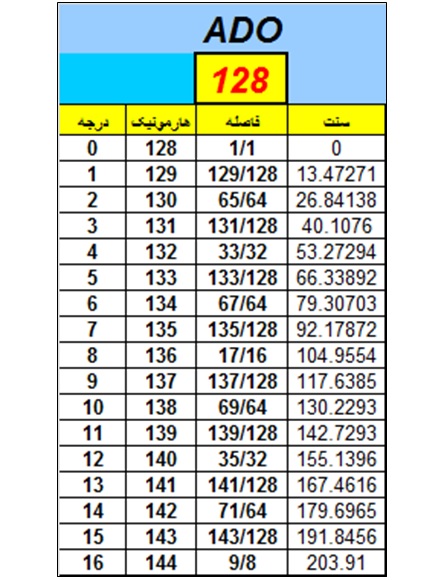
“۱۲۸-ADO” کار می کند. این سیستم فواصل بین هارمونیک های ۱۲۸ تا ۲۵۶ را در بر می گیرد. در جدول زیر بخشی از سیستم “۱۲۸-ADO” را مشاهده می کنیم. در این جدول مشخص است که فاصله هارمونیکی مانند ۱۳۰ با هارمونیک ۱۲۸ معادل فاصله هارمونیک ۶۵ با هارمونیک ۶۴ است:
سری هارمونیک و سیستم فواصل EDL
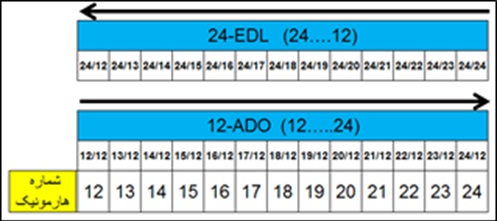
نگارنده قبلا درباره سیستم EDL به طور مفصل نوشته است. در این باره می توان به نوشته «سیستم فواصل تقسیم مساوی طول» درهمین سایت مراجعه کرد. سیستم EDL نیز وابسته به سری هارمونیک است اما با روند معکوس نسبت به سیستم ADO. یعنی در بین هارمونیکهای ۱۲ تا ۲۴ می توان دو سیستم به شکل زیر و با روند معکوس تشکیل داد:
این سیستم بر خلاف سیستم ADO بر اساس تصاعد حسابی شکل نمی گیرد. در سیستم با کاردینالیتی m، درجه a دارای حاصل کسر Ra معادل زیر است:
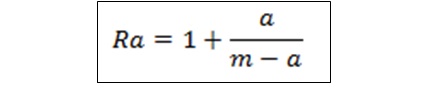
مثلا درجه ۱۱ ام در سیستم فواصل ۲۴-EDL دارای کسری برابر با ۲۴/۱۳ است:
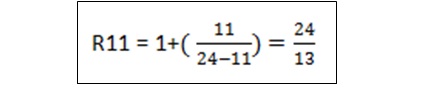
در اینجا نیز نگاهی به روابط طولی پرده بندی در سیستم EDL می اندازیم. در شکل زیر وضعیت طول بخش فعال سیم و پرده بندی را در سیستم ۲۴-EDL مشاهده می کنیم:
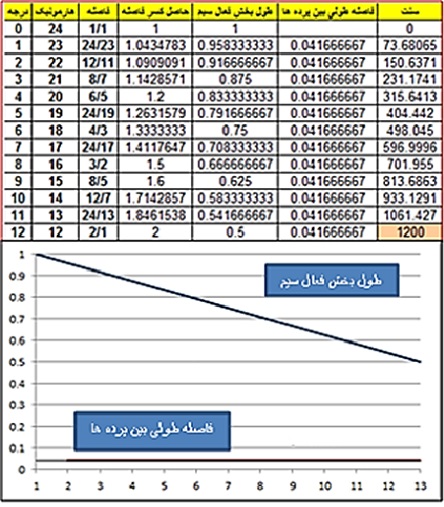
همچنانکه در بخش پایین شکل بالا مشاهده می کنیم، اولین درجه گام دارای طول بخش فعالی معادل طول سیم (با ضریب ۱) بوده و طول بخش فعال درجه مربوط به فاصله اکتاو معادل نصف طول سیم (با ضریب ۰.۵) است. نمودار حاصل از طول بخش فعال سیم و فاصله طولی بین پرده ها نشان دهنده رابطه ای خطی بوده و فاصله طولی بین پرده ها همگی به یک اندازه می باشد.
این سیستم احتمالا از قدیمی ترین سیستم های کوک به کاربرده شده در موسیقی می باشد. طی مکاتبه خصوصی اینجانب با دانشمند شهیر و محقق معروف میکرو تونالیته٬ آقای دکتر جان چالمرز (John Chalmers)، ایشان مشخص نمودند که بطلمیوس (Ptolemy) به هنگام تبیین ساختار تتراکوردی ارائه شده توسط اریستوکسنوس (Aristoxenus)، طول سیم را به ۱۲۰ بخش طولی مساوی تقسیم نموده است. همچنین می توان به مدهای یونان باستان و یا پرده بندی تنبور بغداد بر اساس سیستم EDL اشاره کرد. (نک. سیستم فواصل تقسیم مساوی طول)
به عنوان مثال توصیف موسیقیدان و محقق استرالیایی، السی همیلتون (Elsie Hamilton)، هفت مد باستانی یونان را می توان به شکل زیر در سیستم EDL ارائه داد:
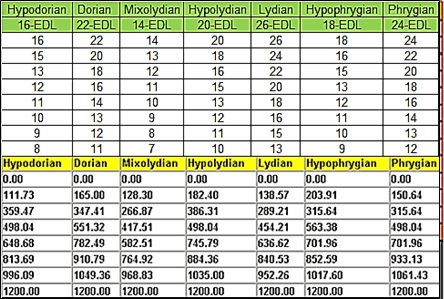
فواصل مد فریژین پس از ساده شدن به صورت زیر نشان داده می شوند:
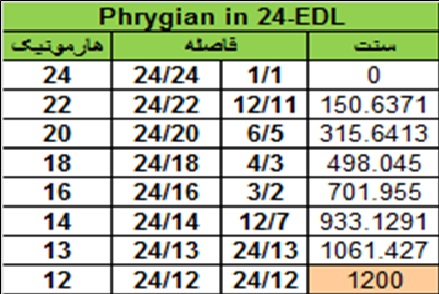
این سیستم فواصل همانند سیستم ADO به شیوه های گوناگون نامگذاری شده است. گاهی می توان آن را به صورت Sub-fm یا Sub-fm-fn نمایش داد:

و البته شاید می توانستند این سیستم را به صورت “Utones fm-fn” نیز نامگذاری کنند (به شرط fm=2fn). به عنوان مثال ۲۴-EDL به صورت Utones 24-12 نشان داده شود.
دلیل انتخاب شیوه نامگذاری (m-EDL) همانند سیستم ADO یکسان سازی روش نامگذاری با سیستم تقسیمات مساوی اکتاو است.
منابع
en.wikipedia.org/wiki/Harmonic_series_(music)
آخرین دسترسی
1396/۱۲/۲۹
en.wikipedia.org/wiki/Sequence
آخرین دسترسی
۱۳۹۶/۱۲/۲۹
fa.wikipedia.org
آخرین دسترسی
۱۳۹۶/۱۲/۲۹
healingfrequenciesmusic.com
آخرین دسترسی
۱۳۹۶/۱۲/۲۹
آخرین دسترسی
۱۳۹۶/۱۲/۲۱
google.com/site/240edo/arithmeticrationaldivisionsofoctave
آخرین دسترسی
۱۳۹۶/۱۲/۲۱
fa.wikipedia.org/wiki
آخرین دسترسی
۱۳۹۶/۱۲/۲۱
xenharmonic.wikispaces.com/Overtone Scales
آخرین دسترسی
۱۳۹۶/۱۲/۲۱
xenharmonic.wikispaces.com/otones8-16
آخرین دسترسی
۱۳۹۶/۱۲/۲۱
huygens-fokker.org
آخرین دسترسی
۱۳۹۶/۱۲/۲۱
آخرین دسترسی
۱۳۹۶/۱۲/۲۱
سیستم فواصل تقسیم مساوی طول
آخرین دسترسی
۱۳۹۶/۱۲/۲۱
Australia’s microtonal modernist: The life and works of Elsie Hamilton
آخرین دسترسی
۱۳۹۶/۱۲/۲۸
THE MODES OF ANCIENT GREECE by Elsie Hamilton
آخرین دسترسی
۱۳۹۶/۱۲/۲۸
8th Octave Overtone Tuning by Johnny Reinhard
آخرین دسترسی
۱۳۹۶/۱۲/۲۸
Barbera ,Andrä.۱۹۹۱. The Euclidean Division of the Canon.univercity of Nebraska





















۱ نظر