ناهمگنی فواصل سیستم EDL درسازهای زهی پرده دار
باید دانست که علی رغم مساوی بودن طول بخش های سیم ٬ ساختار این سیستم دارای تقسیمات اکتاوی غیر مساوی است (می توان آن را جزء سیستمهایی با تقسیمات دارای روند افزاینده Ascending trend دانست). اگر سازی مانند تنبور بغدادی که سیمهایش به فاصله چهارم کوک شده اند را درنظر بگیریم اندازه “فاصله” هر بخش در سیم اول بعد از پرده مربوط به فاصله چهارم با اندازه “فاصله” بخشهای مربوط به سیم دوم که به فاصله چهارم کوک شده است با هم یکسان نمی باشند.
درشکل ۴ اندازه “فواصل بخشها” در تنبور بغدادی محاسبه شده است.
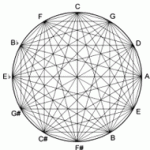
مشخص است که اندازه “فواصل بخشها” در سیستم EDO یکسان است ( شکل ۵) ولی در سیستم EDL روند افزاینده Ascending trend دارد.
به همین دلیل در تنبور بغدادی تتراکورد دوم سیم اول با تتراکورد اول سیم دوم یکسان نمی باشند.
شکل۴ –
هم اندازگی طول بخشهای سیم و ناهم اندازگی اندازه فواصل سیستم EDL درسازهای زهی پرده دار
شکل۵ –
نا هم اندازگی طول بخشهای سیم و هم اندازگی فواصل سیستم EDO درسازهای زهی پرده دار
* ابونصر محمد بن محمد طرخان فارابی
، متولد ۸۷۳ میلادی در فاراب خراسان و متوفی به سال ۹۵۰ میلادی در دمشق، از فیلسوفان بزرگ ایرانی بوده است که به کلیه علوم زمان خویش آگاهی داشته و خصوصا جنبه تئوری و عملی موسیقی را به خوبی می دانست. فارابی در کودکی عود می نواخت و می گویند که ساز قانون نیز از ابداعات او می باشد. او بسیار باهوش و دارای استدلال قوی بوده و به چند زبان رایج زمانه خود تسلط داشته است.
از تالیفات او در زمینه موسیقی می توان کتاب موسیقی کبیر را نام برد که آنرا برای وزیر ابوجعفر محمد بن قاسم کرخی نوشت:” با تشویقت مرا یادآوری کردی به بررسی اجمالی بر آنچه شامل هنر موسیقی می شود که به قدما نسبت داده شده است و از من خواستی که آنرا درکتابی برایت ثبت کنم و بهتر است که در آن شرح و کشفی وجود داشته باشد تا برای خواننده راحت تر شود”.
بیشتر کتابهای فارابی از بین رفته و آنچه برجای مانده است بخش بسیار اندکی است از تلاش آن دانشمند بزرگ ایرانی. فارابی در کتاب موسیقی کبیر بسیار هوشمندانه به توصیف ساختار ساز ها و نحوه پرده بندی و محاسبه فواصل آنها می پردازد. او به نقش کاربرد لگاریتم در محاسبه فواصل موسیقی پی برده و عملا آن را به کار می گیرد. در کتاب موسیقی کبیر٬ سیستم فواصل ۱۲ قسمت مساوی در اکتاو٬ ۱۲-EDO 12-equal divisions of octaveکه همان سیستم ۱۲ نیم پرده معتدل است را تشریح نموده٬ همچنین براساس سیستم ۱۴۴ قسمتی مساوی دراکتاو٬ به تشریح اجناس و مقامهای موسیقی می پردازد. شادروان مهدی برکشلی برهمین اساس ٬ واحد اندازه گیری فواصل موسیقی ٬ فاراب ٬ را که یک درجه از سیستم فواصل ۱۴۴ قسمت مساوی در اکتاو است را به افتخار او معرفی می نماید.
مراجع:
– ابونصر فارابی، الموسیقی الکبیر، ترجمه بافنده اسلامدوست، انتشارات پارت، ۱۳۷۵
–
www.home.austin.rr.com
– فارابی و بقایای پرده بندی پبش از اسلام، بررسی سیستم فواصل طولی در تنبور بغدادی- سال ۸۴- شماره ۶۲- هنرموسیقی



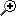




































۱ نظر