فاصله و گام
به طور کلی گام مجموعه ای است از اصوات که فواصل موسیقایی آنها در اکثر اوقات بین ۲ عدد ۱ و ۲ قرار می گیرد. عدد ۱ که اولین درجه گام است پایگی نام داشته و عدد ۲ اکتاو آن است که قاعدتا گام با آن بسته می شود. فرکانس اکتاو ۲ برابر پایگی است :
F2 = 2 × F 1
اکتاو را می توان به اشکال متفاوت تقسیم نمود . مثلا ۱۲ قسمت مساوی که همان گام ۱۲ نیم پرده مساوی است ، ۲۴ قسمت مساوی که گامی ۲۴ ربع پرده مساوی است و …
اگر گام را به ۱۲۰۰ قسمت مساوی تقسیم نماییم به یکی از واحدهای اندازه گیری فاصله درموسیقی دست می یابیم. این واحد سنت CENT نام داشته و با علامت C نمایش داده می شود.
نسبت فاصله موسیقی عبارت است از نسبت فرکانس ۲ نت نسبت به یکدیگر که معادل عددی است بین ۱ و ۲ به گونه ای که :
R=F2/F1 F1 ≤F2
هر فاصله موسیقی را می توان به سنت تبدیل نمود :
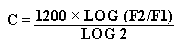
به این ترتیب بین پایگی و اکتاو ۱۲۰۰ سنت و بین دو نت با فاصله پنجم فیثاغورثی (۵/۱ = (R701.9 سنت و بین دو نت با فاصله ۵ در گام ۱۲ قسمتی مساوی ۷۰۰ سنت فاصله وجود دارد.
این نسبتها در واقع بخشی از بی نهایت فاصله موجود در یک گام می باشند چرا که می توان با کوچک کردن میزان سنت بین فواصل آن ها را به هم متصل نمود :

گام فیثاغورثی
فیثاغورث (تولد حدود ۵۶۹ قبل از میلاد در Samos, Ionia ، وفات حدود ۴۷۵ قبل از میلاد)
محل زندگی فیثاغورث در یونان
فیثاغورث به عنوان یک ریاضی دان یونانی تدوین گر نحوه تعیین فواصل و گام موسیقی بر اساس نسبت طولی سیم های کوک شده با فاصله پنجم است. با توجه به پیشرفت ریاضی و موسیقی در مصر و بین النهرین او مطمئنا تحت تاثیراصول موسیقی آموخته شده از مصر و بین النهرین قرار گرفته و بنیاد تئوری خود را بنا نهاده است.
فیثاغورث گام موسیقی را یکی از عناصر ساختاری افلاک می دانست و برای افلاک نوعی آرمونی قائل بود.
همانطور که قبلا ذکر شد، گام فیثاغورث ناشی از ایجاد فواصل پنجم متوالی از یک نت اولیه است. به این ترتیب به دایره ای از فواصل پنجم می توان دست یافت. در شکل زیر دایره فواصل پنجم بر اساس نت دو C در گام ۱۲ نیم پرده مساوی مشاهده می شود:
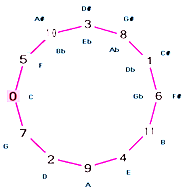
همانطوریکه در شکل بالا مشاهده می شود با حرکت از نت دو به نت سل و بعد به نت ر و نت های دیگر می رسیم . دایره پنجم ها را می توان به صورت
زیر نیز نشان داد
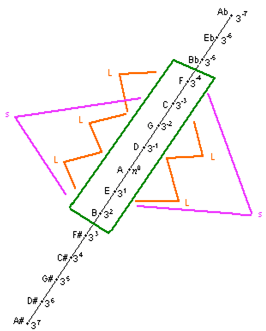
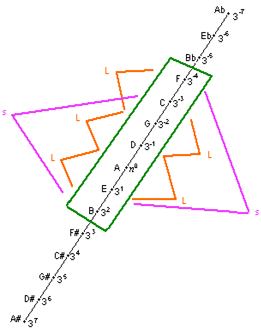
همانگونه که در این اشکال مشاهده می شود فواصل موسیقایی موجو د در کادر همگی تشکیل دهنده یک گام دیاتونیک می باشند. در این گام ۳
فاصله متفاوت وجود دارد:
– پرده L : با نسبت ۹:۸ معادل ۲۰۳.۹۱ سنت .
– نیم پرده دیاتونیک S یا لیما: با نسبت ۲۵۶:۲۴۳ معادل ۹۰.۲۲۵ سنت. لازم به ذکر است که نیم پرده دیاتونیک بین نت های غیر همنام
مانند می و فا مشاهده می شود. (شکل بالا سمت چپ).نیم پرده دیاتونیک را دوم کوچک نیز می نامند و با علائمی مانند min2,
m2, b2 نمایش می دهند.
– نیم پرده کروماتیک یا آپوتوم: اختلاف بین S و L ک معادل ۱۱۳.۶۸۵ سنت یا معادل نسبت ۲۱۸۷:۲۰۴۸ است.
نحوه محاسبه فواصل فیثاغورثی
همانطور که در بالا عنوان شد فواصل فیثاغورثی همگی از تاثیر فاصله پنجم به صورت متوالی و زنجیروار حاصل می شوند. اگر نت پایه را با نسبت
۱:۱فرض کنیم داریم :
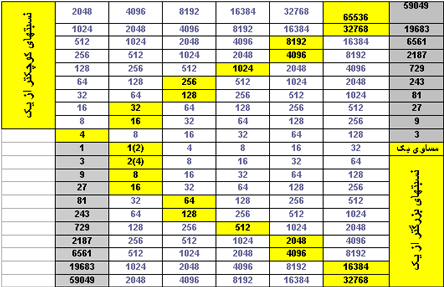
جدول بالا نشاندهنده فواصلی مانند ۳:۲ ، ۸۱:۶۴ ، ۹:۸ ، ۴:۳ ، و غیره است. لازم به ذکر است در ۲ نسبتی که صورت یکی با مخرج دیگری مساوی است رابطه زیر برقرار است:
نسبت کوچکتر= نسبت بزرگتر ÷ ۲
به عنوان مثال :
۴:۳= 3:۲ ÷ ۲
در جدول زیر فواصل فیثاغورثی را در یک گام دیاتونیک مشاهده می نمایید :
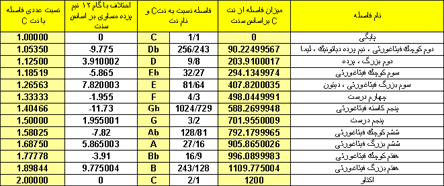
همچنانکه در جدول بالا مشاهده می شود فواصل نیم پرده ای کروماتیک FA# و Sib وجود ندارند. اصولا در این گام فواصلی مانند D# و
Eb باهم برابر نیستند. میزان اختلاف این دو فاصله نیم پرده ای غیر همجنس معادل زیر است :
کومای فیثاغورثی = نیم پرده دیاتونیک(لیما) – نیم پرده کروماتیک(آپوتوم)
۲۳.۴۶سنت = 90.۲۲۵- ۱۱۳.۶۸۵
رابطه گام فیثاغورثی و گام ۵۳ قسمتی مساوی
با توجه به آنکه پرده فیثاغورثی متشکل از لیما و آپوتوم است و با فرض روابط زیر:
پرده بزرگ = آپوتوم + لیما
آپوتوم = لیما + کما
لیما ~ کما ×۴
می توان نوشت :
پرده بزرگ ~ کما × ۹
53 کما ~ ۵ پرده بزرگ + ۲ لیما = اکتاو
به این ترتیب گام فیثاغورثی تقریبا معادل گام ۵۳ کمایی است . با فرض کما معادل ۲۲.۶۴۱ سنت ، گام ۵۳ قسمتی مساوی شکل می گیرد
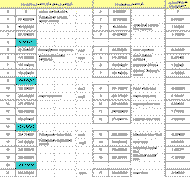
که هر درجه آن برابر با ۲۲.۶۴۱ سنت است. در جدول زیر رابطه گام فیثاغورثی و ۵۳ قسمتی مساوی نشان داده شده است :
با توجه به مقایسه درجات دو گام و فواصل آنها برحسب سنت می توان فهمید که گام ۵۳ قسمتی مساوی جایگزین بسیار مناسبی برای گام فیثاغورثی است .
در همین جا لازم است کمای مرکاتور ( معادل ۳.۱۶۵ سنت ) که کمای دیگری در گام فیثاغورثی است معرفی شود . قبلا گفته شد که هر ۴ کما تقریبا معادل یک لیما است :
کمای مرکاتور (MERCATOR) = لیما – ۴ کما
3.۶۱۵ = 90.۲۲۵ – ۹۳.۸۴
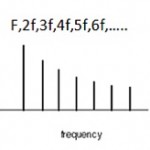
تفاضل درجاتی از گام فیثاغورثی مانند ۴-۹- ۱۵-۲۰ با درجات قبلی خود دقیقا معادل کمای مرکاتور است. در شکل زیر مقایسه بین درجات گام ۵۳ قسمتی مساوی و گام ۱۲ قسمتی مساوی را مشاهده می نمایید. جدول فوق دارای ۱۲ ردیف است که هر ردیف آن معادل ۱۰۰ سنت می باشد :
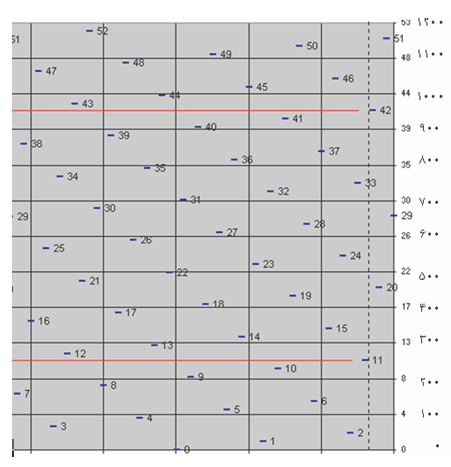
اشکالات سیستم فیثاغورثی
از آنجا که این سیستم زنجیره ای از فواصل پنجم را نشان می دهد ، در انتهای این زنجیره ناهمگنی در انطباق فواصل مشاهده می شود.
به عنوان مثال اگر زنجیره پنجم را با نوت C شروع کنیم داریم :
C-G-D-A-E-B-F#-C#-G#-D#-A#-E#-B#
B# و F# باید آنارمونیک C و F باشند اما اندکی متفاوتند . به همین خاطر در این سیستم به هنگام اجرای مثلا یک پاساژ کروماتیک
مشکل مشاهده می شود .همچنین در مدولاسیون بین کلیدهای مختلف نیاز به نیم پرده های آپوتوم و لیما است.
از مشکلات دیگر این سیستم آن است که فواصلی مانند Eb-G# چهارم درست نبوده و تحت عنوان فاصله چهارم WOLF نامیده
می شوند. فاصله چهارم WOLF از فاصله چهارم درست یک کما (۲۴ سنت) بیشتر است :
(Eb-G#)=(D#-G#)+24c

همچنین فاصله پنجم WOLF در این سیستم ناشی از کاسته شدن یک کما از فاصله پنجم درست می باشد :
(G#-Eb)=(Ab-Eb)-24c
لغت WOLF احتمالا مربوط به سونوریته ارگ های بادی اولیه است که به هنگام نواختن چنین فواصلی به گوش شنوندگان شبیه صدای
زوزه گرگ به نظر می رسد.
احتمالا تغییرات در ساختار سیستم فیثاغورثی از قرن ۱۴ میلادی شروع شده است. دراین زمان جایگاه نیم پرده های آپوتوم و لیما عوض
شده و به صورت زیر در آمد :
(C) 90 –(C#/Db)– ۱۱۴ (D)
با گذشت زمان انواع سیستم های اعتدال نیز ابداع گردید تا بتوانند نقائص این سیستم را بر طرف نمایند.این امر در نهایت به سیستم اعتدال
12 نیم پرده مساوی انجامید که در قبل ذکر گردید.



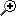



































aalist.
بابا یه خورده آروم تر ! فهمیدن اینها یه خورده به زمان نیاز داره!
khaste nabashid. kheili mofid bood
اینا رو تو دانشگاه موسیقی هم یاد می دن؟؟؟ واقعا یه دنیاییه…
من از ریاضی فراریم و عاشق موسیقی.. می بینم که باید ریاضی رو خوب بلد باشم تا موسیقی رو خوب یاد بگیرم…
baba dametoon garm in noskheye ghabele chap ke on balast kheili bahale
واقا عالیست .متاسفانه موسیقی اصیل را با موزیکهای یک شبه عوض کردن .من فیزیک خوندم ÷ معرکه است این سایتتون
fogholadas. baraye man ke kheili mofid bud.
fogholadas. baraye man ke kheili mofid bud.
nazarate ostad Kiani ra besyar mipasandam
ممنون ولی واقعا سنگینه
به نظر من موسیقی از هر علمی بهتره. چون هم فیزیکه هم ریاضیه هم فلسفه ست هم پزشکیه هم معارفه و خیلی چیزای دیگه.
از مطالبی که مینویسید خیلی خوشم میاد بیشتر اطلاعات داشته باشم. ادامه بدید. دستتون درد نکنه…
mamnon kheili baram mofid bood
سایت جامع و کاملیه،لذت بردیم.موفق باشید
چه میکنه این مقالات هارمونی تاک –
واقعاً مقالات این سایت هم از لحاظ کمیت ه م کیفیت خوبن – دمتون جمیعاً گرم
با سلام.واقعا که مرسی .بسیار از این مقاله خوشم اومد.کاملا مفید برای همه اونایی که میخوان موسیقی را با تلاش فراوان دنبال کنند همچین مجموعه ها و مقالاتی خیلی خیلی به درک اونها از موسیقی میانجامد.لینک های فراوون دیگه ای رو هم دیدم که حتما به اونها سر میزنم
عالی بود اینو میگن ارتباط موسیقی با ریاضی!!
سلام
دوست عزیز لطفا با یک موسیقی دان مشورت کنید و با همکاری ایشان این مسائل را توضیح دهید
ظاهرا شما فیزیکدان هستید
ممنون