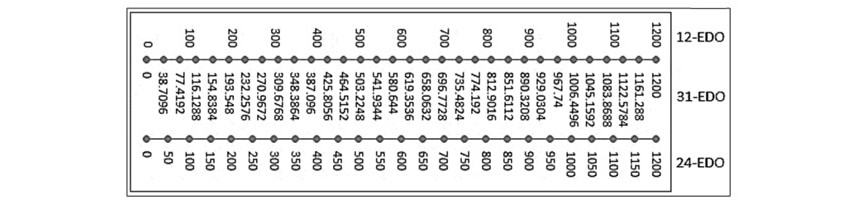
گام ۱۲ قسمتی
گام ۱۲ قسمتی، گامی است که از دوازده قسمت در یک اکتاو تشکیل شده است. این گام میتواند دارای فواصل مساوی یا نامساوی باشد. گام ۱۲ قسمتی مساوی یا (۱۲-EDO (12 Equal divisions of Octave دارای ۱۲ فاصله نیم پرده ای مساوی است:
C-(C#/Db)-D-(D#/Eb)-E-F-(F#/Gb)-G-(G#/Ab)-A-(A#/Bb)-B-C’
کوتاه درباره موسیقی شانسی و پیشینه آن
در موسیقی تصادفی و شانسی، آهنگساز با روشهایی تصادفی -مانند شیر یا خط یا انداختن تاس- به گزینش نوتها، آکوردها، صداهای زیر و بم، ریتمها و رنگهای صوتی می پردازد. در اینگونه آثار همچنین ممکن است از اجراکنندگان خواسته شود تا ترتیب و آرایش یا حتی بخش عمده مواد موسیقایی را خود برگزینند. برای نمونه، ممکن است آهنگساز بخشی کوتاه از اثر را به نگارش درآورد و از اجراکننده بخواهد تا آن را به ترتیب دلخواه خود بنوازد یا امکان دارد که با اشاره به گروهی از صداهای زیر و بم، اجراکننده را در ابداع الگوهایی ریتمیک بر آن مبنا راهنمایی کند. (کیمی ین، ۱۳۸۰، ۷۲۳)
گنجاندن عناصر شانس در آهنگسازی و اجرای موسیقی شانسی چیز جدیدی نیست؛ قطعاتی که بتوان آنها را پیشینهای برای آهنگسازی شانسی در نظر گرفت، حداقل به اواخر قرن پانزدهم برمیگردد. “Musikalisches Würfelspiel” یا بازی موزیکال تاس در اواخر قرن ۱۸ و اوایل قرن ۱۹رایج گشت. اینگونه بازیهای تاس به کارل فیلیپ امانوئل باخ، فرانتس جوزف هایدن و ولفگانگ آمادئوس موتزارت نسبت داده میشود. در بازیهای تاس موزیکال، از دو تاس استاندارد ششوجهی استفاده میشود تا عبارات کوتاه موسیقی را به روشهای تصادفی بههم متصل کنند.
در قرن بیستم، ایوز، بولز و اشتکهاوزن، همگی عمدتاً با واگذاری جنبههای خاصی از فرم به نوازنده، تا حدی از تصادفی بودن در کار خود استفاده کردند. با این حال، جان کیج، در استفاده از عناصر شانسی مانند استفاده از تاس در هنگام آهنگسازی پیشگام بود.
نتنگاری قطعه پیانویی شماره ۱۱ از اشتوکهاوزن (۱۹۵۶) از نوزده تکه کوچک چاپشده بر طوماری کاغذی به اندازه ۹۴ در ۵۳ سانتیمتر تشکیل شده است. این تکهها میتوانند به هر ترتیبی نواخته شوند و از اجراکننده خواسته شده با نخستین تکه نت که میبیند قطعه را آغاز کند. به این ترتیب، متفاوت بودن قطعه در هر اجرا محتمل میشود. (کیمی ین، ۱۳۸۰، ۷۲۴)
ریاضی و موسیقی
هنر محصول تلاش انسان برای بیان تجربیات زندگی است. در این میان، بهدلیل اشتراکات ریاضی و هنر، ریاضیدانان در طول تاریخ ابزار فراوانی را برای بیان تجربیات زندگی در اختیار بشر قرار دادهاند. از جمله میتوان به خلاقانهبودن، ماهیت انتزاعی و در جستجوی زیبایی بودن اشاره کرد (Budd,2020). ریاضی، گشاینده رازهای قوانین زیبای طبیعت است. از نظر گالیله، هنرمندانی که بهدنبال مطالعه طبیعت و بهرهگیری از آن در بیان تجربیات زندگی خود هستند، باید ریاضی را درک کنند. (Shara,2022) داوینچی همواره به اهمیت ریاضی و نسبتهای هندسی در خلق آثار هنری معتقد بود و رازهایی مانند فرمها و الگوهای هندسی که از طریق بررسیهای علمی خود آشکار شده بود را در آثار نقاشی خود القا میکرد (آتالای،۱۳۹۶،۱۹۰).
کار ریاضیدانان شباهت زیادی با کار هنرمندان دارد؛ نقاش رنگها و فرمها را بههم میآمیزد، موسیقیدان اصوات را، شاعر واژهها را و ریاضیدانان نوع خاصی از ایدهها را (برل، ۱۳۹۷). ریاضی میتواند اعداد، نسبتها و تقارنهای پنهان را بیرون کشیده و در دسترس هنرمند قرار دهد. هنرمند با دستیابی به چنین مهارتهای ریاضی، میتواند شگرد کشف نسبتهای موجود در طبیعت را بهدست آورده و دامنه تخیل هنری و از جمله موسیقایی خود را گسترش دهد. این اتفاق بهنوعی مبین شکلگیری مسیری نو بین علم و موسیقی است، مسیری که خلاقیت فیالبداهه و ناآگاه هنرمند را، بهسمت اندازهگیری و بهرهگیری از واقعیات عینی هدایت میکند.




























۱ نظر