کاربرد دایره در ایجاد گام‌های 12 قسمتی میکروتونال (4) – گفتگوی هارمونیک

2- سیستم فواصل زاویه ای
همانطور که قبلا اشاره شد، هر کمان در دایره یک زاویه مرکزی به دست می دهد. مجموع زوایای مرکزی در دایره معادل ۳۶۰ درجه است. از طرفی می‌توان فرض کرد که کل دایره معادل ۱۲۰۰ سنت است. به این ترتیب هر درجه معادل ۳. ۳۳ سنت و هر سنت برابر با ۰. ۳ درجه خواهد شد. در نهایت می‌توان یک سیستم فاصله دیگر بر اساس زوایای مرکزی مرتبط با هر کمان در دایره مشخص نمود. برای این کار زوایای مرکزی مرتبط با هر کمان را طبق فرمول زیر به دست آورده:

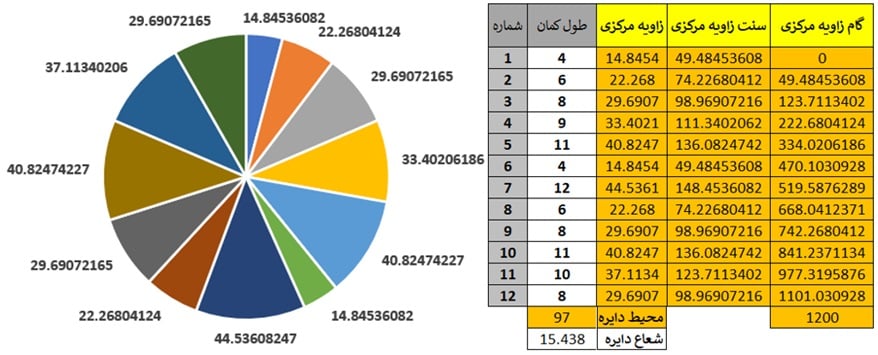
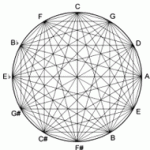
شکل۱۰: از راست به چپ: – اندازه فواصل سیستم زاویه ای – موقعیت ۱۲ زاویه داخلی بر روی دایره و اندازه آنها (منبع نگارنده)

۳- سیستم فواصل وتری
پاره‌خطی که دو نقطه متمایز از محیط یک دایره را به هم پیوند می‌دهد، وتر (d) آن دایره نامیده می‌شود. وترهای متصل به هم در داخل دایره یک چندضلعی محاطی (چند ضلعی که همه راس‌های آن بر روی دایره قرار دارد) را ایجاد می نمایند. به این ترتیب اساس محاسبه سیستم فواصلی که بر اساس اتصال وترهای موجود در دایره شکل می گیرد همانند محاسبه فواصل یک دوازده ضلعی خواهد شد (مهاجری، ۱۴۰۳). برای این کار جمع طول وترها یا محیط چند ضلعی محاطی را معادل طول اکتاو بر روی یک سیم (طول سیم فرضی دو برابر محیط چند ضلعی است) فرض می‌کنیم. با محاسباتی همانند محاسبه فواصل یک دوازده ضلعی می‌توان سیستم فواصل بر اساس وترهای موجود را به دست آورد. برای محاسبه طول وترها براساس زاویه مرکزی و یا طول کمان از روابط زیر استفاده می‌شود:

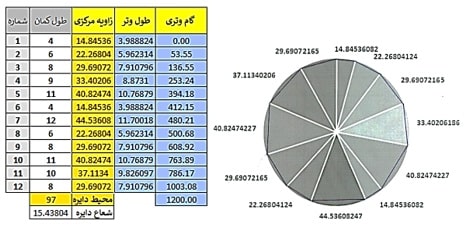
پس از محاسبه طول وترها براساس زاویه مرکزی و یا طول کمان، می‌توان فواصل حاصل از چند ضلعی محاطی به دست آمده (گام وتری) را محاسبه نمود (شکل۱۱):

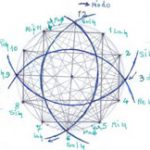
شکل ۱۱: از راست به چپ: – موقعیت ۱۲ ضلعی محاطی – جدول نشان دهنده فواصل گام وتری و طول ۱۲ وتر (به همراه کمانها و زوایای مرکزی مربوطه) (منبع نگارنده)

شکل زیر، مقایسه این سه نوع سیستم فواصل را نشان می دهد (شکل۱۲):

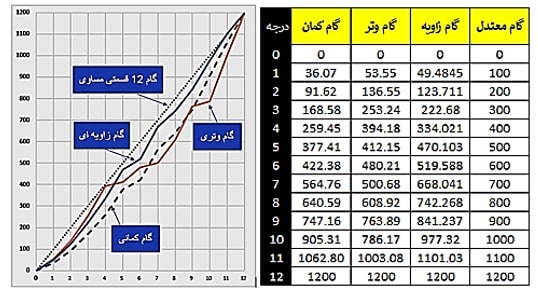
شکل ۱۲: جدول و نمودار مقایسه ای فواصل چهار گام ۱۲-EDO، وتری، زاویه ای و کمانی (منبع نگارنده)

نتیجه گیری
همچنانکه در یک تحقیق مشخص شده است (مهاجری، ۱۴۰۳)، انواع ۱۲ ضلعی در طراحی گام های ۱۲ قسمتی میکروتونال کارایی دارند. در این نوشته پس از بررسی یک دایره با ۱۲ کمان بر روی خود، مشخص شد که می‌توان حداقل سه سیستم فاصله ۱۲ قسمتی میکروتونال از دل آن بیرون کشید. در ادامه این گونه تحقیقات می‌توان به کاربرد ۱۲ضلعی های محیطی (۱۲ ضلعی محیطی، یک چندضلعی است که همۀ اضلاع آن بر یک دایره مماس‌اند) و نقش بیضی در طراحی گام نیز پرداخت. این موضوعات اهمیت ریاضی و به خصوص هندسه اشکال متنوع را در طراحی گام های میکروتونال، بیشتر نشان می دهد.

پیوست
بر‌اساس نتایج حاصل از استخراج گام زاویه ای ۱۲ قسمتی میکروتونال از دایره ذکر شده در مقاله، یک قطعه موسیقی ساخته و ارائه می‌شود (شکل۱۳). برای ساخت این قطعه با انتخاب سمپل و بعد از ورود اندازه فواصل در سمپلر “Kontakt”، نوت‌نویسی در برنامه Encore 4. 5 انجام می‌شود. در این لینک، امکان دسترسی به قطعه فراهم شده است. شیوه نت‌نویسی قطعات میکروتونال منطبق بر روش پیشنهادی نگارنده می‌باشد (مهاجری، ۱۳۹۳).