کاربرد دایره در ایجاد گام‌های ۱۲ قسمتی میکروتونال (۳)

همچنانکه گفته شد، دایره یک منحنی مسطح و بسته شامل نقاطی از صفحه است که فاصله‌شان از نقطه ثابتی واقع در آن صفحه به نام مرکز مقداری ثابت است. می‌توان چنین تصور کرد که یک پاره خط همواره می‌تواند با اتصال ابتدا و انتهایش تشکیل یک دایره دهد. به این ترتیب طول پاره خط معادل محیط یک دایره شده و از طرفی تقسیمات طولی ایجاد شده بر روی پاره خط معادل کمان‌های دایره می‌شوند (شکل۶):

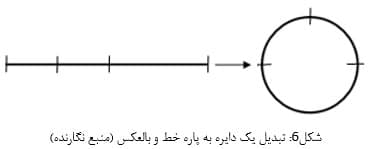
بنابراین محیط کمان بندی شده یک دایره را می‌توان به یک پاره خط با تقسیمات طولی تبدیل کرده و به اولین سیستم فواصل ناشی از دایره که یک سیستم از فواصل از جنس تقسیمات طولی است، دست یافت. همچنین میدانیم که هر کمان در دایره یک زاویه مرکزی به دست می‌دهد. مجموع زوایای مرکزی در دایره معادل ۳۶۰ درجه است. از طرفی می‌توان فرض کرد که کل دایره معادل ۱۲۰۰ سنت است. به این ترتیب هر درجه معادل ۳. ۳۳ سنت خواهد شد و در نهایت می‌توان یک سیستم فاصله دیگر بر اساس زوایای مرکزی مرتبط با هر کمان در دایره مشخص نمود (شکل۷):

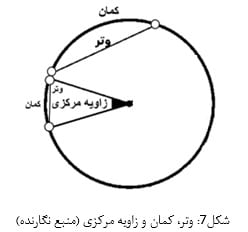
همچنانکه در شکل بالا مشخص است هر زاویه مرکزی مولد یک کمان و وتر است. وتر در واقع پاره‌خطی است که دو نقطه متمایز از محیط یک دایره را به هم پیوند می‌دهد. وتر های متصل به هم در داخل دایره، یک چندضلعی محاطی (چند ضلعی که همه راس های آن بر روی دایره قرار دارد) را ایجاد می نمایند (شکل۸):

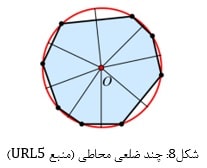
با کمک چند ضلعی محاطی در درون دایره نیز می‌توان به سومین سیستم فاصله از جنس تقسیمات طولی دست یافت. به این ترتیب هر دایره حداقل سه سیستم فاصله به دست می‌دهد:
1- سیستم فواصل کمانی: سیستم فواصل بر اساس کمان‌های موجود بر روی محیط دایره
2- سیستم فواصل زاویه‌ای: سیستم فواصل بر اساس زوایای مرکزی دایره
3- سیستم فواصل وتری: سیستم فواصل بر اساس وترهای مرتبط با کمان و زوایای مرکزی (تشکیل دهنده چند ضلعی محاطی)

۱- سیستم فواصل کمانی
اگر یک دایره را که محیطش دارای ۱۲ کمان است، از محل اتصال دو کمان اش (که آن را مبدا می‌نامیم) باز کنیم، به پاره خطی تبدیل می‌شود که می‌توان آن را به یک دوازده ضلعی تبدیل نمود. به این ترتیب اساس محاسبه سیستم فواصلی که بر اساس اتصال کمان‌های موجود بر روی محیط دایره شکل می‌گیرد همانند محاسبه فواصل یک دوازده ضلعی خواهد شد (مهاجری، ۱۴۰۳). برای این کار طول محیط دایره را معادل طول اکتاو بر روی یک سیم (طول سیم فرضی دارای طولی دو برابر محیط دایره است) فرض می‌کنیم. با محاسباتی همانند محاسبه فواصل یک دوازده ضلعی می‌توان سیستم فواصل بر اساس کمان‌های موجود را به دست آورد.

مثال:
دایره ای داریم به شعاع ۱۵. ۴۳۸ سانتی متر و محیط ۹۷ سانتی متر. بر روی این دایره ۱۲ کمان را مطابق جدول زیر مشخص می‌کنیم. با محاسباتی همانند محاسبه فواصل منتج از یک دوازده ضلعی (مهاجری، ۱۴۰۳) می‌توان سیستم فواصل گام منتج از کمان‌های دایره زیر را به دست آورد (شکل۹):

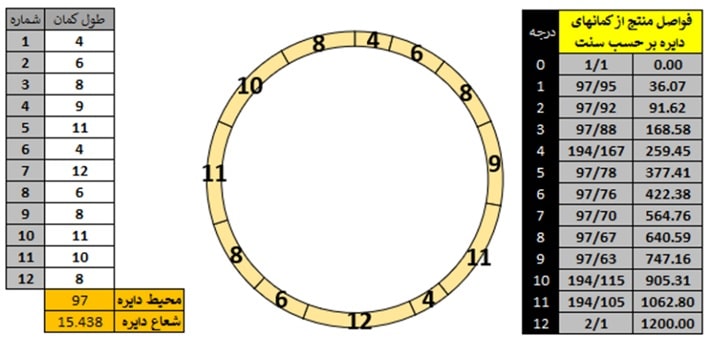
شکل۹: از راست به چپ: – اندازه فواصل سیستم کمانی – موقعیت ۱۲ کمان بر روی دایره – جدول نشان دهنده طول ۱۲ کمان (منبع نگارنده)