در این مقاله، به کاربرد تابع یک متغیره، به عنوان یکی از مفاهیم ریاضی، در طراحی گامهای میکروتونال پرداخته میشود. تفکر ریاضی میتواند روابط و نسبتهای موجود در دل پدیدهها را بیرون کشیده و خلاقیت هنرمند را به سمت اندازهگیری و ایجاد آنچه میخواهد، هدایت کند. در موسیقی نیز وجوه قابل اندازهگیری و تحلیل براساس ریاضی فراواناند. بررسی امکان طراحی سیستمهای فواصل موسیقی، از طریق مدلسازی براساس یک تابع ریاضی میتواند کاربرد ریاضی در موسیقی را پراهمیتتر جلوه دهد. هدف این نوشته، بررسی امکان و ارائه راهکار در مورد نحوه به کارگیری توابع یک متغیره برای ایجاد گامهای میکروتونال است. برای این منظور، ابتدا به مبانی نظری شامل بررسی ماهیت گام و سیستم فواصل، موسیقی میکروتونال، رابطه ریاضی و طبیعت و هنر، رابطه ریاضی و موسیقی پرداخته و سپس پیشینه مطالعات و امکان و نحوه استفاده از توابع ریاضی در طراحی گامهای میکروتونال با استفاده از ”Desmos Studio” و یک کاربرگ محاسباتی و فرمول نویسی شده در نرم افزار “Excel” بررسی میشود. در انتها براساس نتایج حاصل، یک قطعه موسیقی ارائه میشود. برای ساخت این قطعه، سمپلی انتخاب و بعد از ورود اندازه فواصل در سمپلر “Kontakt”، نتنویسی در برنامه “Encore 4.5” انجام میشود.
واژه های کلیدی
گام میکروتونال، سیستم فواصل، تابع یک متغیره
مقدمه
موسیقی میکروتونال، موسیقی است که در آن، از فواصل موسیقایی متفاوتی در مقایسه با گام رایج ۱۲ نیمپرده مساوی استفاده میشود. طراحی سیستمهای فواصل میکروتونال، از جنبههای خلاقانه موسیقی میکروتونال است. ریاضی در شکلگیری سیستم فواصل مانند سیستمهای فیثاغورثی، کوک میانه، نقش اساسی دارد. سوالی که مطرح میشود این است که آیا مفاهیمی مانند توابع ریاضی میتوانند مبنای خلاقیت و ایدهپردازی در طراحی و مدل سازی گام قرار گیرند؟
در این مقاله ابتدا به اختصار، به مبانی نظری شامل بررسی ماهیت گام و سیستم فواصل، موسیقی میکروتونال، رابطه ریاضی و طبیعت و هنر، رابطه ریاضی و موسیقی پرداخته و سپس پیشینه مطالعات و امکان و نحوه استفاده از توابع ریاضی در طراحی گامهای میکروتونال بررسی و چند قطعه شنیداری ارائه میگردد.
روش تحقیق
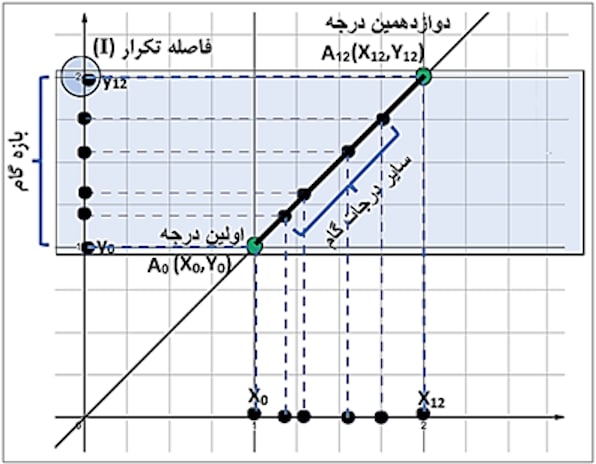
در این تحقیق که دارای هدفی کاربردی بوده و به روش تحلیلی انجام میشود، پس از بررسی پیشینه مطالعات و انتخاب مثالهایی از انواع مختلف توابع و رسم نمودار آنها در نرمافزار “Desmos Studio”، داده های حاصل از محاسبات در یک کاربرگ محاسباتی و فرمولنویسیشده “Excel” وارد شده و فواصل و گامهای ۱۲ قسمتی میکروتونال مربوط به هر تابع به دست میآید.





























۱ نظر