ریاضی میتواند اعداد، نسبتها و تقارنهای هر پدیدهای را بیرون کشیده و در دسترس هنرمند قرار دهد. به این ترتیب:
- ریاضیدانان، موسیقی را همواره به عنوان موضوعی برای تحقیق علمی فرض کرده و در نتیجه مجموعهای از ایدههای نظری و تجربی و مدلسازیهای متنوع به وجود آمده است. محاسبات ریاضی سیستمهای کوک ار جمله این ایدههای نظری و تجربی است.
- هنرمند نیز با دستیابی به چنین مهارتهای ریاضی، میتواند با مدل سازیهای خاص خود، ابزار و قلمرو تخیل موسیقایی خود را گسترش دهد.
نقش ریاضی در محاسبه فواصل موسیقی غیر قابل انکار بوده و از دیر باز موسیقی به عنوان ابزاری پرکاربرد، محاسبات فواصل و سیستم های کوک را پیش برده است. در زیر به ذکر مثالهایی پرداخته میشود:
۱- یکی از قدیمی ترین شیوههای محاسبه فواصل، کاربرد چرخه پنجم بالا رونده و پایین رونده و به دست آوردن نسبتهای کسری فواصل است. علیرغم ارتباط منطقه بینالنهرین با این روش (۲۰۲۱,۹۷، De Rose)، به دلیل نقش پررنگ فیثاغورث (۵۷۰ـ۴۹۵ پم) در کاربرد این شیوه، این محاسبات به نام او ثبت شده است (۲۰۰۹,۱۴،Fauvel &Flood & Wilson).
۲- آرخوتاس تارِنتومی، فیلسوف یونانی مکتب فیثاغورثی (۴۲۸ـ۳۴۷پم)، به کاربرد سه میانگین هندسی، ریاضی و هارمونیک در محاسبه فواصل موسیقی به غیر از چرخه فاصله پنجم اشاره کرده است (۱۹۶۴، Crocker).
۳- آریستوکسنوس (۳۷۵ـ۳۳۵پم)، فیلسوف و ریاضیدان یونانی و شاگرد ارسطو، به عنوان اولین کسی که نظام کوک فیثاغورثی را مردود دانسته و به سمت طراحی اعتدال مساوی حرکت کرد (۱۹۵۱,۲ ،Barbour)، با اندازهگیری فاصله معادل ۱۲/۱ پرده، به محاسبه فواصل گام ۷۲ قسمتی مساوی پرداخت (Macran, 1902). البته برخی از محققین معتقدند که او محاسبات سیستم فواصل ۱۴۴ قسمتی مساوی را نیز ارائه کرده است (Monzoe, 2003)، همان سیستمی که فارابی در کتاب موسیقی کبیر خود و در بحث تقسیم متناسب به آن پرداخته است (۱۹۹۶,۶۸ ,Farabi).
۴- محاسبات لئونارد اویلر، ریاضیدان و فیزیکدان سوئیسی، در اندازهگیری میزان مطبوع بودن فواصل موسیقی (۲۰۱۳، Pesic).
۵- تلاش جوزپه زارلینو، نظریهپرداز موسیقی و آهنگساز اهل جمهوری ونیز در دوره رنسانس، برای جبران بدصدایی فواصل سیستم فیثاغورثی و تعریف و محاسبه فواصل سیستم درست “just” براساس کاربرد فاصله سوم و ششم بزرگ طبیعی در کتاب “Institutioni harmoniche” درسال ۱۵۵۸ (۲۰۰۹,۲۰،Fauvel & Flood & Wilson).
۶- ارائه محاسبات ریاضی سیستم فواصل کوک میانه “Meantone” توسط فرانچسکو سالیناس، موسیقیدان اسپانیایی درسال ۱۵۷۷ و در کتاب “De musica libri septem” برای جبران بهتر مشکل مدولاسیون در سیستم فواصل درست (Ibid, 23).
۷- تلاشهای رنه دکارت، ریاضیدان، دانشمند وفیلسوف عقل گرای نامدار فرانسوی عصر روشنگری در سال ۱۶۱۸ و دررساله Compendium music )به معنای خلاصه موسیقی( جهت محاسبه فواصل موسیقایی به صورت نسبتهای ریاضی (Ibid, 3).
۸- ویلیام بروکنر، مترجم کتاب دکارت به زبان انگلیسی، اولین ریاضیدان انگلیسی بود که لگاریتم را (اختراع شده در سال ۱۶۱۴) در محاسبات تقسیمات فواصل موسیقی به کار برده و یافتههای دکارت را به چالش میکشد (Ibid).
۹- نیوتن، ریاضیدان و فیزیکدان انگلیسی ، با آموختن همه آن چیزهایی که توسط ریاضیدانان مدرن مانند دکارت ارائه شده بود، در مطالعات خود به سرعت از آنها فراتر رفت و تقسیمات مساوی مختلفی برای اکتاو از جمله ۶۱۲ تقسیم را در نظر گرفت (۲۰۲۱، MUZZULINI).
۱۰- انجام محاسبات و پیشنهاد گام ۵۳ قسمتی مساوی توسط نیکولاس مرکاتور، ریاضیدان آلمانی قرن (۱۷۳۱,۷۹ ،Holder).
۱۱- محاسبه فواصل انواع سیستمهای اعتدال خوب “well temperaments” از طریق اصلاح سیستمهای فواصل کوک میانه برای ایجاد امکان مدولاسیون بهتر درتمام گامها (با کمک ایجاد تغییر اندازه بعضی از فواصل پنجم و سوم) (۲۰۲۳ ،Broekaert).
۱۲- در طول تاریخ و در نقاط مختلف دنیا، تلاشهایی برای محاسبه فواصل سیستم ۱۲ نیم پرده مساوی انجام شده است که شاید بتوان محاسبات نیوتون در مورد گامی با دوازده نیم پرده مساوی (Adams,2014) و محاسبات سایمون استیون، ریاضیدان اهل فلاندر بلژیک، در سال ۱۶۰۵ و در کتاب ناتمام Van de Spiegheling der singconst” (1605، Stevin)” را مهمترین آنها دانست. آنها پیشنهاد داند که از ریشه ۱۲ام عدد دو برای محاسبه نیم پرده استفاده شود (Adams,2014) و (۲۰۰۹,۲۵،Fauvel & Flood & Wilson).
۱۳- فارابی، فیلسوف و موسیقیدان ایرانی (۸۷۸-۹۵۰) درکتاب موسیقی کبیر، روش محاسبات عددی مرتبط با فواصل موسیقایی را به تفصیل شرح داده است (۱۹۹۶,۷۹ ,Farabi). او همچنین، مانند اریستوکسنوس، به محاسبات تقسیمات مساوی و از جمله تقسیم گام به ۱۴۴ قسمت مساوی آگاه بوده است (۱۹۹۶,۶۸ ,Farabi).


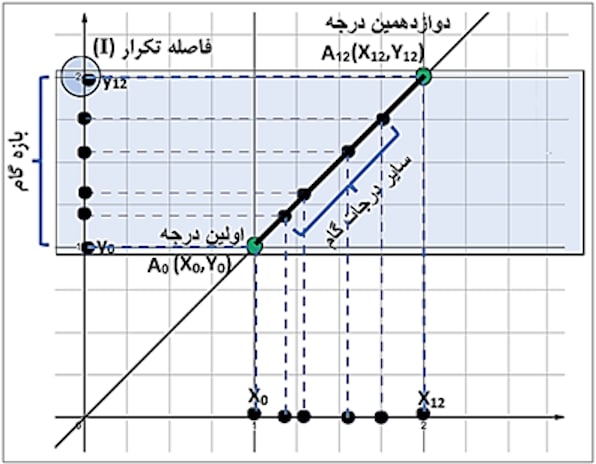



























۱ نظر