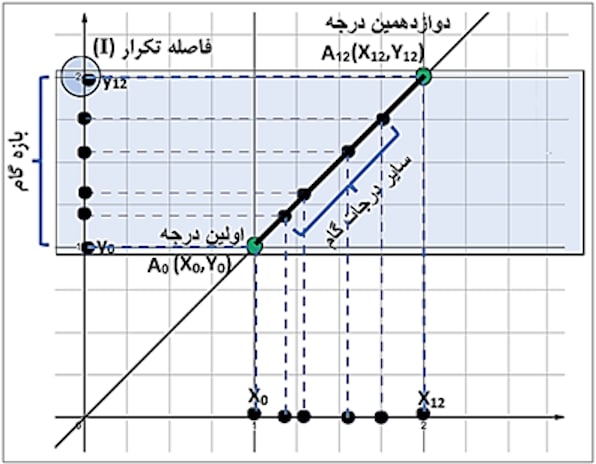
- نمودار تابع (Graph of a function): یکی از روشهای متداول برای نمایش توابع ریاضی، رسم نمودار آنها است. در این روش، معمولا ازصفحه مختصات دکارتی “Cartesian coordinate system” یا دستگاه مختصات دوبعدی با محور افقی x و محور عمودی y استفاده میشود. برای رسم نمودار، به تعدادی جفت مرتب (x,y) نیاز است. به همین دلیل، مقادیر قلمرو تابع (x) را در فرمول یا ضابطه تایع قرارداده و مقادیر متناظر برد تابع (y) را به دست میآوریم. جفت مرتبهای حاصله را در دستگاه مختصات دوبعدی رسم کرده وآنها را به هم وصل میکنیم تا نمودار تابع به دست آید.
توابع ریاضی، انواع بسیار گستردهای دارند. از انواع آنها میتوان به تابع یک متغیره، تابع جبری، تابع چندجملهای با درجه n، تابع گویا، تابع معکوس، تابع نمایی، تابع توانی، تابع لگاریتمی وغیره اشاره کرد. توابع همچنین میتوانند زوج یا فرد، صعودی یا نزولی، معکوس و پوشا باشند (جدول۲):

پیشینه تحقیق
علی رغم اینکه عمده کاربرد ریاضی در مبحث کوک و فواصل، توصیف ریاضی شکلگیری سیستمهای فواصلی مانند سیستم فیثاغورثی است، اما میتوان انواعی از گامهای موسیقایی، به خصوص گامهای میکروتونال را مشاهده کرد که فرمولهایی خاص برای طراحی آنها ارائه شده است. با اینحال، هیچ صراحتی در مورد نقش این فرمولها به عنوان تابع ریاضی یا اصولا امکان کاربرد توابع در طراحی گام، مشاهده نمیشود:
- کاربرد ریشه ۱۲ام عدد ۲ برای محاسبه فاصله نیم پرده در گام ۱۲ قسمتی مساوی
در این پیشنهاد که اساس شکل گیری گام ۱۲ قسمتی مساوی بوده و توسط اسحاق نیوتون (Adams ,2014) و سپس توسط سایمون استیون ( ۲۰۰۹,۲۵،Fauvel & Flood & Wilson) مطرح شد، نیم پرده معادل ریشه ۱۲ام عدد ۲ (برابر عددی تقریبا معادل ۱.۰۵۹۴۶۳) است:
![]()
فواصل دیگر گام نیز از ضرب متوالی عدد معادل فاصله نیم پرده شکل میگیرند. به عنوان مثال فاصله دوم بزرگ (به عنوان نوت سوم گام با درجه ۲)، برابر است با:
![]()
اولین درجه گام نیز به شرط اختصاص عدد ۰ به آن برابر است با:
![]()
به این ترتیب، تمام درجات گام ۱۲ نیم پرده مساوی (با فرض نوت C به عنوان نوت آغازین گام) طبق جدول زیر (جدول ۳) محاسبه میشوند:

علی رغم آنکه نیوتون و استیون در زمان خود، فرمولی را برای محاسبه فواصل گام دوازده قسمتی مساوی ارائه نکرده بودند، اما میتوان تابع نمائی زیر را برای این محاسبه در نظر گرفت:






























۱ نظر