شاهین مهاجری
گام میکروتونال ۱۲ قسمتی اشنایدر با ماهیت لگاریتمی
روبرت اشنایدر، در تلاش برای طراحی یک گام با ماهیت غیرفیثاغورثی، گامی میکروتونال و ۱۲ قسمتی با ماهیت لگاریتمی را طراحی نمود (۲۰۱۳، Schneider). او با فرض فرکانس نوت C4 معادل ۲۶۴ هرتز، فرمولی را ارائه داد که میتوان آنرا برای محاسبه فرکانس درجات گام بهکاربرد:
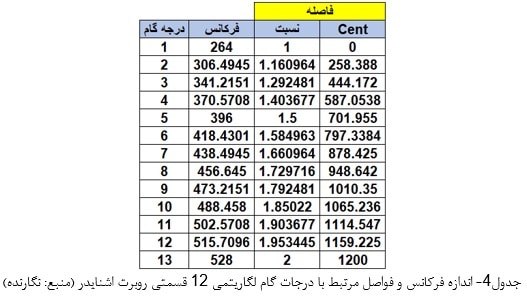
در این فرمول، F معادل فرکانس درجهای از گام بوده و به x نیز مقادیری از ۱ تا ۱۳ تعلق میگیرد. به این ترتیب، فرکانس و فاصله تمام درجات گام ۱۲ قسمتی او (با فرض نغمۀ C=264 Hz به عنوان نغمۀ آغازین گام) طبق جدول زیر (جدول ۴) محاسبه میشوند:
- فرمولهایی مرتبط با انواعی از گامهای میکروتونال
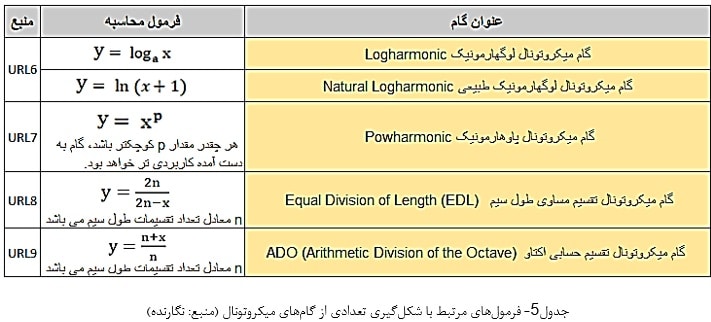
در جدول زیر میتوان فرمولهایی مرتبط با شکل گیری انواعی از گامهای میکروتونال را مشاهده نمود (جدول۵):
بررسی نحوه کاربرد توابع تک متغیره در طراحی گام های میکروتونال
همچنانکه از مثالهای بالا مشخص است، ساختار تعدادی از سیستمهای فواصل به وسیله فرمولهایی خاص تعریف شدهاند. در این فرمولها، همواره یک ورودی مستقل و یک خروجی وابسته وجود دارد. در هر کدام از آنها، به ازای مقداری برای ورودی مستقل میتوان مقداری متناسب برای خروجی وابسته به دست آورد. به این ترتیب، این فرمولها عملا تابع ریاضی هستند، بدون آنکه هیچ تصریحی در مورد تابع بودن آنها یا اصولآ تاکید بر امکان کاربرد توابع در طراحی گام، مشاهده شود.
در اینجا ماهیت تابعی ۳ نمونه از فرمولهایی که قبلا درمورد نحوه محاسبه فواصل در این تحقیق مورد اشاره قرار گرفتند، مجددآ یادآوری میشوند:
- در فرمول گام پیشنهادی اشنایدر (فرمول ۷)، میتوان با انتخاب درجات گام از ۱ تا ۱۳ به عنوان ورودی مستقل x، مقادیر متناسبی را برای خروجی وابسته F که فرکانس نغمههای گام است، به دست آورد. بنابراین فرمول اشنایدر نوعی ضابطه یا تابع است که در آن مقادیر y (فرکانس نوتهای گام) به مقادیر x(درجات گام) بستگی دارد (جدول۴). این تابع، تابعی لگاریتمی و تک متغیره است که قلمرواش، بازه [۱,۱۳] از اعداد طبیعی N و برد آن مجموعه اعداد اعداد حقیقی مثبت R+ میباشد. با حذف عدد ثابت ۲۶۴ در تابع گام اشنایدر (فرمول ۷)، میتوان به فرمولی رسید که نسبتهای فواصل موسیقایی را به دست دهد (فرمول ۸). به این تریتب داریم:
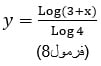
2- فرمول محاسبه فواصل گام دوازده قسمتی مساوی (فرمول ۶) نوعی تابع نمائی تک متغیره است (فرمول ۹):
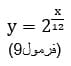
قلمرو این تابع نمایی، بازه [۰,۱۲] از اعداد طبیعی N و برد آن بازه [۱,۲] از اعداد حقیقی مثبت R+ میباشد.۳- فرمول محاسبه فواصل بر حسب سنت (Cent) (فرمول۲) نیز نوعی تابع لگاریتمی تک متغیره است (فرمول ۱۰):
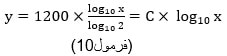
دراین سه تابع معرفی شده، اگر خروجی y را معادل فاصله موسیقایی بدانیم، میتوان فرض کرد که تابع ریاضی میتواند برای طراحی سیستم فواصل موسیقی مورد استفاده قرار گیرد. برای طراحی سیستم فواصل، نیاز به یک روش محاسباتی میباشد که شیوه زیر مراحل محاسبه را شرح میدهد:
1- انتخاب نوع گام: اولین مرحله در طراحی، انتخاب نوع گام به صورت اکتاوی یا غیراکتاوی است.
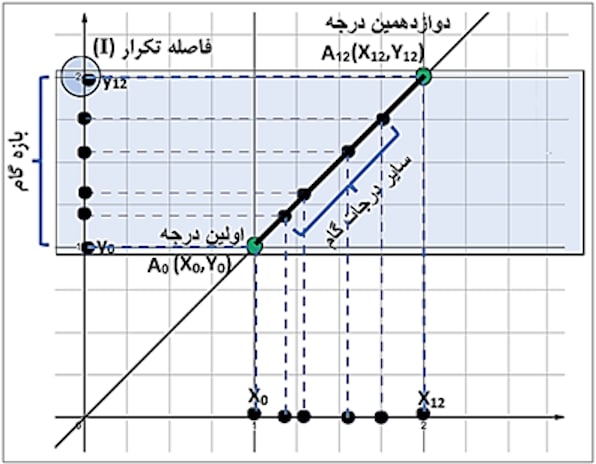
2- انتخاب فاصله تکرار و بازه گام: همچنانکه قبلا عنوان شد، فاصله تکرار I، فاصلهای است که گروه فواصل توسط آن تکرار میشود. این فاصله در گام اکتاوی، اکتاو و در گامهای غیراکتاوی، هر فاصلهای به غیراز اکتاو میتواند باشد. بدیهی است که طراحی گام توسط تابع، در بازهای از محور y به صورت [۱,I] به نام بازه گام انجام میشود. عدد ۱ در این بازه گویای فاصله اولین درجه گام (درجه صفر) و عدد I مبین فاصله تکرار (درجه ۱۲ ام گام) است.
3- مشخص کردن جفت مرتب اولین و دوازدهمین درجه گام: هرنقطه از بازه [۱,I] بر روی محور y دارای x متناظر خود بر روی محور x بوده، به گونه ای که زوج مرتبهای ابتدا و انتهای بازه، مربوط به اولین درجه [x0,y0] و دوزادهمین درجه [x12,y12] مربوط به میباشند. x های این دو زوج مرتب نتیجه حل ضابطه تابع در دو نقطه y0=1 و y12=I هستند (شکل ۲).
4- مشخص کردن جفت مرتبهای بقیه درجات بین اولین و دوازدهمین درجه گام: برای مشخص شدن جفت مرتبهای درجات بین اولین و دوازدهمین درجه گام، ابتدا باید x های یازده درجه باقی مانده را براساس x های درجات اول و دوازدهم به دست بیاوریم. برای این کار میتوان روشهای مختلفی را به کار برد اما در یک روش، میتوان ابتدا قدرنسبت m را محاسبه نمود (فرمول۱۱):
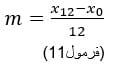
سپس با استفاده از تصاعد حسابی زیر (فرمول ۱۲)، مقدار x برای درجه D ام گام محاسبه میگردد:
۱ نظر