یکی از مهمترین مسایل در موسیقی و سایکوآکوستیک، تحقیق پیرامون خوش صدایی و بد صدایی است. تاکنون نظرات مختلفی در این مورد ابراز گشته است اما طبق نظر ویلیام ا.ستاریس (William A. Sethares) رابطه منطقی بین ساختار هارمونیک صدا و خوش صدایی در یک قطعه موسیقایی، در یک گام خاص وجود دارد.
او که متولد سال ۱۹۵۵ بوده و به عنوان یک تئوریسین موسیقی، در دانشگاه ویسکانسین آمریکا استاد رشته مهندسی برق می باشد، در مورد تئوری خوش صدایی (Consonance) نظرات جالبی مطرح کرده است. مجموع نظریات او را در چندین مقاله مانند: “Adaptive tunings for musical scales” که در مجله انجمن آکوستیک آمریکا در سال ۱۹۹۴ منتشر شده و در کتاب: “Tuning, Timbre, Spectrum, Scale” و همچنین در وبسایت اش می توان مشاهده نمود.
او معتقد است مفهومی مانند خوش صدایی کاملا تابع دو فاکتور ساختار هارمونیک صدای برآمده از ابزارمولد صوت و ساختار فواصل گامی است که موسیقی بر اساس آن ساخته شده است. وی اساس کار خود را بر اساس مدل خوش صدایی “Plomp” و “Levelt” بنا نهاد که معتقد بودند: «خوش صدایی می تواند مبتنی بر ساختار هارمونیک صدا باشد.» ستاریس براساس معادلات ریاضی و گراف های حاصله نشان می دهد که در جهت رسیدن به حداکثر خوش صدایی:
۱- برای هر ساختار گام باید صدایی با ساختارهارمونیک متناسب با آن گام طراحی کرد.
2- برای هر ساختار هارمونیک می توان گامی خاص را مشخص نمود.
بر اساس مدل “Local consonance” او معتقد است که صدایی با ساختار هارمونیک شامل نسبتهای زیر:
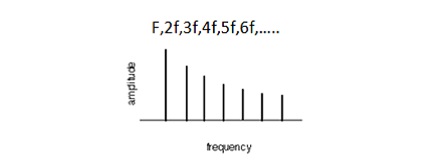
بهترین خوش صدایی را نه در گام معتدل ۱۲ نیم پرده مساوی که در گامی بر اساس فواصل طبیعی نشان می دهد. در شکل زیر می توان فهمید که به هنگام همصدایی دو صدا با فواصل مختلف، فواصل هم صدا و اکتاو و پنجم بسیار خوش صدا بوده در عین حالی که هرچه فرکانس صدای دوم از فاصله همصدا بیشتر شود، میزان بدصدایی (Dissonance) طبق نظر “Plomp” و “Levelt” بیشتر می شود.
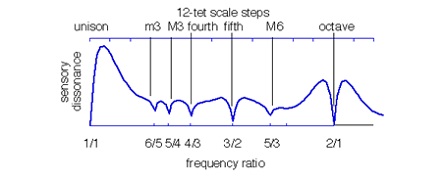
طبق مدل ویلیام ا.ستاریس، ساختارهارمونیک صدا در صورتی با یک ساختار گام مرتبط است که نقاط حداقل در نمودار بد صدایی جزیی از درجات آن گام باشند که در شکل بالا این نقاط نه با گام معتدل بلکه با گام طبیعی هماهنگی دارد.
در یک آزمایش جالب یک صدا با دومولفه هارمونیک که هارمونیک اول دارای فرکانس f و صدای دوم دارای هارمونیک ۱.887749f ( معادل هفتم بزرگ معتدل) است طراحی کرده و آن را به وسیله نرم افزار “Kontakt” به یک گام گسترش می دهیم. دراین آزمایش معلوم می شود که نتایج محاسبات ستاریس صحیح بوده و تغییرات خوش صدایی در طول یک اکتاو صدا منطبق بر منحنی حاصله است:
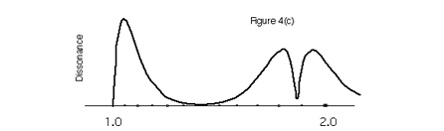
در این مثال درجه اکتاو کاملا بد صدا بوده در عوض درجه هفتم بزرگ معتدل در همصدایی با درجه اول (به دلیل وجود هارمونیک دوم ۱.887749f معادل هفتم بزرگ معتدل) خوش صداست که در شکل بالا در درجه هفتم یک حداقل بد صدایی مشخص است. جالب آنکه در حول و حوش چهارم افزوده نیز به دلیل کاهش ملایم بد صدایی می توان خوش صدایی نسبی را شنید. به مثال های مرتبط گوش دهید:
1-
درجات هفتم و اکتاو همزمان با درجه اول؛
در این مثال دو صدایی مبتنی بر اکتاو بسیار بد صدا تر از دوصدایی مبتنی بر درجه هفتم است. (اول دوبل با درجات هفتم و بعد دوبل با درجات اکتاو را می شنوید)
۲-
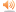
توالی درجات گام ماژور همزمان با درجه اول
۳-
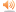
قطعه ملودی کوچکی در چهارگاه معتدل

اما ابتکار دیگر ستاریس مبتنی بر طراحی گام براساس نمودار خوش صدایی است. او بر اساس ۷ هارمونیک ساختار صدای زیلوفون که توسط “Fletcher and Rossing” به صورت زیر ارائه شدند:
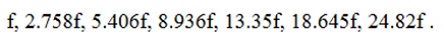
نمودار خوش صدایی زیر را رسم کرده و فواصل درجات گام را براساس نقاط حداقل بد صدایی بدست آورد:
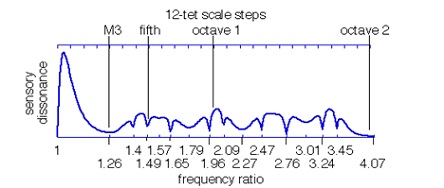
ستاریس همچنین پیشنهاد می دهد که برای ساخت موسیقی بر اساس سیستم های چند قسمتی مساوی ساختار هارمونیک صدا بر اساس درجاتی از این سیستم ها طراحی شود. در یک مثال او سیستم ۱۰ قسمتی مساوی را در نظر گرفته و هارمونیک های زیر را برای ساختار صدا در نظر می گیرد:
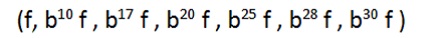
با فرض اینکه b ریشه m ام عدد ۲ می باشد هرکدام از این هارمونیکها درجه ای از گام ۱۰ قسمتی مساوی هستند. در این گام b معادل ۱.۰۷۱۷ است. در جدول زیر فرکانسهای مربوط به ۷ هارمونیک را که در طراحی یک نمونه صدا به کار رفته مشاهده می کنیم:
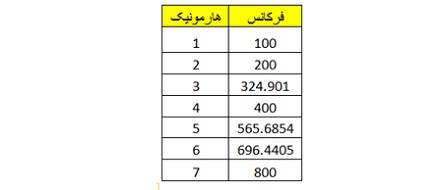
منحنی خوش صدایی این صدا در گام ۱۰ قسمتی مساوی از خود چندین نقطه با حداقل بد صدایی را نشان می دهد:
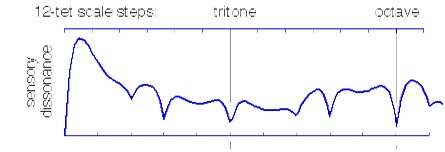
در زیر یک نمونه صوتی از گام ۱۲ قسمتی مساوی را می شنویم که با این نمونه صدا اجرا شده است و در ادامه آن همان ملودی که به گام ۱۰ قسمتی مساوی منتقل شده است. واضح است که ساختار صوتی در گام ۱۰ قسمتی مساوی خوش صدا تر است.
توالی درجات گام ماژور همزمان با درجه اول
در نهایت ستاریس معتقد است مدل خوش صدایی او با توجه به مشکلات ساخت سازهای آکوستیکی با این مشخصات هارمونیک می تواند به راحتی توسط سینتی سایزرها و دنیای موسیقی دیجیتال و الکترونیک به گوش برسد. تصور شنیدن موسیقی در گامهای مختلف که هر کدام توسط صداهایی با ساختارهارمونیک خاص خود گام طراحی شده اند جذاب است.






































۱ نظر