مدلی برای کد گذاری مدهای نیم پرده ای و میکروتونال ناشی از گامهای اکتاوی ۱۲درجه ای
مقدمه
مدهای نیم پرده ای و میکروتونال (ناشی از گامهای ۱۲ درجه ای نیم پرده ای یا میکروتونال اکتاوی) در یک مورد مشابهت دارند: نحوه آرایش درجات مد. گامهای ۱۲ درجه ای مختلف میکروتونال را میتوان به شیوه های مختلف طراحی نمود. این شیوه ها کاربرد الگوریتمهای مختلف ریاضی تا استفاده از هارمونیک ها در سطوح مختلف را در بر میگیرند.
همانند سیستم ۱۲ نیم پرده مساوی که دارای مد های متعدد موسیقایی در فرهنگ های مختلف موسیقایی است گامهای میکروتونال ۱۲ درجه ای نیزمی توانند مد های گوناگونی را بر اساس انتخاب درجات گوناگون درمحدوده اکتاو به وجود آورند.
با توجه به تنوع و گوناگونی گامها و همچنین تعدد مدهای ناشی از یک گام و وجود مدهایی با درجات یکسان ولی نامهای متفاوت، نیاز به یک روش کدگذاری یکدست برای شناسایی مد های میکروتونال احساس میشود. این روش باید:
1- فارغ از اندازه مطلق فواصل گام باشد. نام گذاری باید صرفا گویای موقعیت نسبی درجات و فواصل مد نسبت به هم باشد و نه اندازه آنها.
۲- این سیستم باید به گونه ای باشد تا به راحتی تجسمی از ساختار مد را به دست دهد.
ایده طراحی این مدل توسط این جانب از ساختار دانگ و گامهای دیانونیک و کروماتیک ناشی شده است. این مدل همچنین در مورد کد گذاری مد های مختلف برآمده از سیستم ۱۲ نیم پرده مساوی کاربرد دارد.
درجه و فاصله
اساس این مدل دسته بندی درجات یک گام می باشد. در تعریف درجه Degree باید گفت که هر نت موجود در یک گام یک درجه ازآن می باشد به این ترتیب گام هپتاتونیک دارای ۷ درجه می باشد (همانند تعداد درجات گام دیاتونیک ). درجات می توانند متصل مانند درجه ۱ و۲ یا منفصل باشند مانند درجات ۱و۷. باید توجه داشت که آخرین درجه هر گام (همانند درجه ۱۲ گام کروماتیک) در واقع اولین درجه گام در تکرار خود است.
اما تفاوت درجه و فاصله در این است که بین هر دودرجه (چه متصل چه منفصل) یک فاصله مشاهده میشود. بنابراین گام ۷ درجه ای ۷ فاصله دارد.
بخش
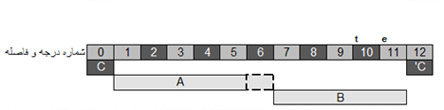
برای دستیابی به ساختارهای ۷ درجه ای و دیگرازدرون ساختار گام ۱۲ درجه ای میتوان درجات آن را دسته بندی کرد تا آن را به دو بخش A و B تقسیم کرد.

با توجه به شکل بالا موارد زیرمشخص میشود:
1- یک اکتاو ۱۲درجه ای به دو بخش مساوی A و B تقسیم شده است. هر کدام دارای ۵ فاصله بوده و بین آنها یک فاصله بینابینی مشاهده می شود. این فاصله بینابینی(۶ امین فاصله) می تواند به بخش A اضافه شود.
۲- موقعیت نسبی فواصل نسبت به درجه صفر که نت آغازین گام است محاسبه میشود. در این سیستم همانطوریکه در ابتدا عنوان شد اندازه مطلق فاصله به هیچ عنوان مطرح نمی باشد. به این ترتیب در بخش A عدد ۲ مبین دومین فاصله نسبت به مبداء گام است فارغ از اندازه آن. ۳- برای شماره گذاری فواصل از اعداد یک رقمی استفاده شده است. در بخش B برای اعداد ۱۰ و ۱۱ به پیشنهاد Arnold Whitall در کتاب
The Cambridge Introduction to Serialism از جایگزین هایی مانند t و e استفاده شد.
نحوه کد گذاری
کد گذاری هر مد از یک گام تابع تعداد و شماره درجات انتخابی از گام است. به مثال زیر که در مورد یک گام هپتاتونیک است دقت کنید:

مثال بالا نشان می دهد که این مد در بخش A دارای درجات ۲-۴-۵ و در بخش B دارای درجات ۷-۹-۱۱ است..هر۲بخش بدون درنظر گرفتن اندازه فاصله درواقع مبین نوعی دسته بندی و انتخاب از بین درجات گام اند به گونه ای که حالت موسیقایی خاصی را نشان دهند. نکته مهم آن است که این ۶ درجه را به شیوه های مختلف میتوان از بین درجات انتخاب نمود. به این ترتیب و بر اساس اندازه فاصله های بین درجات این بخشها می توانند مساوی یا نامساوی باشند.
نحوه نمایش کد گذاری
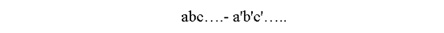
نمایش کدینگ در این مدل به شکل زیر است:
a,b,… معرف درجات و فواصل انتخاب شده هستند. دو بخش توسط خط تیره از هم جدا شده اند. مسلم است بخش اول A در سمت چپ کدینگ قرار دارد.
در مورد مثال بالا این فرمول به شکل زیر کد مد را نشان می دهد:

تعداد حروف تابعی از تعداد فواصل هر بخش درمد مورد نظر است. در مورد مد های مختلف اندازه فواصل به شرح ذیل است:
مد ۸ درجه ای اکتاتونیک…. ۸ فاصله
مد ۷ درجه ای هپتاتونیک…. ۷ فاصله
مد ۶ درجه ای هگزاتونیک…. ۶ فاصله
مد ۵ درجه ای پنتاتونیک…. ۵ فاصله
در زیر چند مثال را در ساختار سیستم ۱۲نیم پرده مساوی مشاهده می نمایید:

گام هپتاتونیک آدونای مالاخ در موسیقی عبری با کدینگ



گام اکتاتونیک Bebop dominanth با کدینگ

این مثال نمونه ای است از ساختارمد با بخشهای نامساوی.


گام پنتاتونیک هیراجوشی در موسیقی ژاپن با کدینگ

این مثال نمونه ای است از ساختارمد با بخشهای نامساوی.


گام تمام پرده با کدینگ


مد فریژین با کدینگ


حال در زیر به بررسی کاربرد کدینگ ارائه شده در یک نمونه سیستم میکروتونال مانند سیستم ۲۴-EDL پرداخته میشود.
سیستم میکروتونال 24-EDL
این سیستم میکروتونال که دارای ۱۲ درجه در اکاست بر اساس تقسیم مساوی طول سیم به ۲۴ قسمت طولی مساوی شکل میگیرد. در شکل زیر مقایسه ایست بین سیستم ۱۲ درجه ای ۲۴-EDL و سیستم ۱۲ نیم پرده مساوی EDO-12:
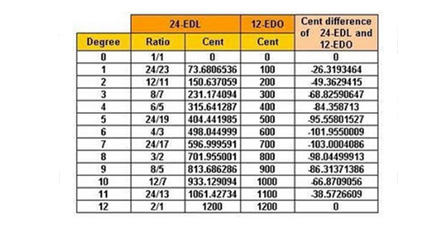
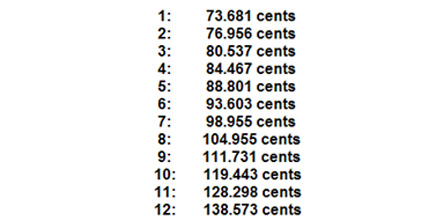
اندازه فواصل بین درجات متصل در سیستم ۱۲ نیم پرده مساوی همگی برابر ۱۰۰ سنت Cent است در حالی که این اندازه در سیستم 24-EDL متغیر و افزایشی است:
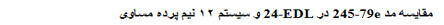
ساختار این مد در سیستم ۱۲ نیم پرده مساوی نشاندهنده ساختار مد ماژور است فارغ از مشخصات مدال این مد. حال در جدول زیر به مقایسه این ساختار و فواصل آن در این دو سیستم می پردازیم: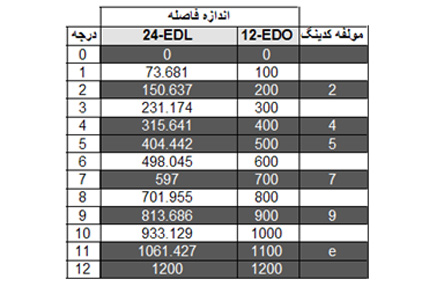
در زیر به مثالی از این مد که در این دو سیستم اجرا میشود گوش کنید و متوجه تفاوت حالت موسیقایی آنها بشوید. این تفاوت به دلیل نا همگونی اندازه فواصل متعلق به درجات متناظر در این دو مد می باشد.
اجرا در سیستم ۱۲ نیم پرده مساوی
اجرا در سیستم ۲۴-EDL

همچنانکه دیده میشود این مدل کدینگ یک ساختار مد را در دو سیستم مختلف فاصله نشان می دهد بدون آنکه بر اندازه فواصل تاکید کند. به نظر می رسد این مدل بتواند در مشخص کردن مدهای مختلف موسیقایی فارغ از اندازه فواصل و کارکرد مدال آنها کارایی داشته باشد.






























با سلام
سوالی از خدمت شما داشتم. البته قبلش باید بگم چون بنده زیاد با قواعد میکروتنالیته آشنا نیستم شاید در انتخاب بعضی کلمه ها اشتباه داشته باشم که خیلی ممنون میشم اگر این اشتباهات رو به بنده تذکر بدید. اما موضوع اصلی:
در زمینه فواصل موسیقی ایرانی نکته ای هست که مدت طولانی ذهن بنده رو درگیر کرده. شما سیستم فواصل 96EDO رو برای این موسیقی پیشنهاد کردید تا نظر هر دو تفکر موجود در مورد فواصل ایرانی (که همه به اون واقفیم) رو برآورده کنید. اما در مواردی این سیستم دچار انحرافاتی هست. مثلا در زمینه درجه سوم گام شور (مثلا سی بمل در شور سل) معمول هست که حدودا فاصله ۲۹۴ سنتی (۳۲/۲۷) رو کوک کنند. (یعنی مثل سوم کوچک فیثاغورث) اما در فواصل 96EDO این فاصله به ۲۸۷.۵ تقلیل پیدا میکنه که به نظر زیاد خوب از آب در نمی آد. حالا اگه سیستم تقسیم مساوی طول معادل 96EDO رو در نظر بگیریم (که میشه 192EDL) فواصل معمول در موسیقی ایرانی به شکل خیلی بهتری به دست می آد. مثلا برای همون دستگاه شور درجات ۱۵ – ۳۰ – ۴۸ – ۶۴ – ۷۱ – ۸۴ – ۹۶ . که به جز درجه ۷۱ که به مقدار کمی از فاصله معمول بیشتره (حدود ۵ سنت) باقی فواصل عینا موجود هستند. حالا سوالی که برای من هست اینه که اولا آیا 192EDL معادل 96EDO هست یا بنده دچار کج فهمی شدم؟ و بعد اینکه آیا میشه گفت فواصل موسیقی ایرانی با سیستم فواصل تقسیم مساوی طول بهتر بیان میشه؟؟
امیدوارم که زیاد “یاوه” نگفته باشم!!
با تشکر…
سینای عزیز
مرسی از اینکه وقت گذاشتی … اتفاقا خیلی خوشحال میشم که با هم بحث کنیم … عزیز
1 – از نجایی که حد تفکیک یاJND گوش به طور میانگین بین ۵ تا ۱۰ سنت است
http://en.wikipedia.org/wiki/Pitch_(music)#cite_note-Olson-2
زیاد “فرقی معنی دار” بین ۲۹۴ و ۵۸۷.۵ سنت با اختلاف ۶.۵ سنت وجود ندارد …. میشه اینو آزمایش کرد.
2- سیستم EDL با سیسیتم EDO هیچ ارتباط ماهیتی ندارد بنابراین ۱۹۲ هم ارتباطی با ۹۶ ندارد.
سینای عزیز البته یادم رفت اسمم را در پست قبلی بنویسم.
اول تشکر می کنم بابت لطفتون و همینطور ممنون از اینکه برداشت اشتباه چند ساله من بابت سیستم EDL و EDO رو اصلاح کردید!! حالا اصل موضوع:
من فکر میکنم نوشته ام یه کمی گنگ بود و منظورم رو گویا نرسوند. من منظورم از زیاد خوب نبودن به صورت تئوری بود. وگرنه برای گوش درک این تغییرات خب امکان پذیر نیست. حتی اساتید موسیقی هم وقتی کوک می کنن بسته به اینکه اون ساز چه فاصله ای رو بهشون تحمیل کنه یا دلایل دیگه تا همین حدود JND اختلاف خواهند داشت. برای همین اگه اجازه بدید برداشت خودم رو از فواصل ایرانی بگم تا بتونم بهتر از شما کمک بگیرم:
من اینطور گمان می کنم که چون بخش بزرگی از موسیقی ایرانی ذاتا تکنوازیه باید فواصل این موسیقی در خودش ملایمت consonanse داشته باشه. چیزی که اگر اشتباه نکنم میگن فواصل هارمونیک یا طبیعی. چون من سازم سنتوره، برای کوک کردن این ساز از همین ملایمت ها استفاده می کنیم و اونطور که میدونم در اکثر سازها هم همینطوره (البته با احتساب همون حد تفکیک گوش) به فرض ما اول سل رو از دیاپازن کوک می کنیم. بعد فاصله چهارم رو کوک می کنیم(مثلا دو). حالا بنده اینطور فکر میکنم که ملایم ترین فاصله چهارم ۴/۳ هست. پس دو میشه ۴۹۸.۰۴ بالاتر از سل. به همین ترتیب دو تا سل اکتاو بعدی فاصله پنجمه که ملایمترینش ۳/۲ هست که پس سل اکتاو بعدی ۱۲۰۰ سنت بالاتر از سل اولی میشه. ملایمترین فاصله پرده هم ۹/۸ هست که پس فا میشه -۲۰۳.۹. و چهارم فا هم میشه سی بمل که هست ۳۲/۲۷ بالاتر از سل یا ۲۹۴.۱۳.
بعد ربع پرده ها هم به فرض سه گاه رو که در نظر بگیریم با استفاده از فا می تونیم لاکرن رو کوک کنیم که اگه از ۱۱/۹ استفاده کنیم هم فا تا لا کرن (۱۱/۹) و هم لاکرن تا دو (۲۷/۲۲) و هم لا کرن تا سی بمل (۱۲/۱۱) همه ملایمترین حالات هستند که فکر میکنم تمام این فواصل به اسم فواصل خنثی neutral شناخته میشن. و این رویه پیدا کردن ملایمترین فاصله رو برای تمامی فواصل هم میشه انجام داد. چون مثلا در شهناز شور همین فواصل حاکمه. یا در چهارگاه معمولا فرود لاکرن دو خیلی خوب چهارگاه رو نشون میده و در کل این فاصله سوم خنثی neutral third در موسیقی ایرانی خیلی استفاده میشه و …
حالا نمی دونم اصلا چنین کاری درسته یا نه؟ اما من نتیجه رو با یک نرم افزار که میکروتنال داره (Harmony Assistant) انجام دادم که لااقل به گوش من خوب اومد. ممنون میشم دوباره اشتباهاتم رو تذکر بدید.
مرسی سیناجان
خیلی خوبه .. داری بر اساس سیکل بالارونده و پایین رونده پنجم کار می کنی … اصولا باید سیستم خودت رو پیدا کنی …. البته بهتره با نرم افزار scala هم کار کنی:www.huygens-fokker.org/scala/
و به این سایت هم سری بزن
http://www.tonalsoft.com
خوشحالم که به این موضوع علاقه مندی …
موضوعی که باید روش تمرکز کنی درمورد فواصل کسر دار موضوع limit هست که خیلی جالبه .. تو همون تونال سافت پیگیرش شو … موفق باشی ..