ضربان Beating: ضربان تغییر متناوب و ریتمیک حجم صوتی است به دلیل تداخل Interference دو موج صوتی با فرکانس بسیار نزدیک به هم.

میزان این تغییر حجم یا واحد ضربان در واحد ثانیه BPM یا Beat per minute سنجیده می شود و برابر است با تفاوت دو فرکانس. به عنوان مثال دو موج سینوسی ۱۰۰ و ۱۰۴ هرتز ضربانی با سرعت ۴ بار در ثانیه تولید می کنند.
در شکل زیر تغییر متناوب حجم صوتی را به صورت تغییر در شکل موج مشاهده می کنید:
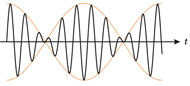
به هنگام کوک دو سیم ساز به صورت همصدا به راحتی می توان متوجه این حالت شد.
دو نت با فرکانس های F1 و F2 که F2>F1 است را در نظر بگیرید.
این دو صدا نسبت به هم C سنت فاصله داشته و این فاصله به یک فاصله طبیعی F3=A/B نزدیک می باشد.نحوه محاسبه ضربان بین این دو صدا عیارت است از:
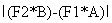
به عنوان مثال ضربان بین دو نت دو و سل که فاصله ۷۰۰ سنت نسبت به هم دارند به شکل زیر محاسبه می شود:
فرکانس نت دو= 261.۶۳ Hz
فرکانس نت سل با فاصله ۷۰۰ سنت از نت دو= 392.۰۰۲۰۸ Hz
ضربان بین دومین هارمونیک سل و سومین هارمونیک نت دو = l(392.00208*2)-(261.63*3)l=0.8858 BPM
پس بین دومین هارمونیک نت سل و سومین هارمونیک نت دو ضربانی با میزان ۰.۸۸۵۸ BPM ایجاد می گردد.
۲- محدوده Limit: نظریات Harry Partch 1974-۱۹۰۱ در مورد محدوده ها یکی از مطالب جالب در کاربرد فواصل گویا و طبیعی می باشند.
محدوده بزرگترین عدد اولی است که توان غیر صفر داشته و حاصل از تجزیه عدد اصلی می باشد . صورت و مخرج هر کسری را میتوان به اعداد اول تجزیه نمود. اعداد اول ، اعدادی می باشند که به غیر از ۱ و خودش بر عدد دیگری تقسیم نشود. به اعداد زیر دقت کنید :
00000،۸۳،۷۹،۷۳،۷۱،۶۷،۶۱،۵۹،۵۳،۴۷،۴۱،۳۷،۳۱،۲۹،۲۳،۱۹،۱۷،۱۳،۱۱،۷،۵،۳،۲
عددی مانند ۱۳ به غیر از ۱ و خودش بر هیچ عدد دیگری قابل تقسیم نمی باشد . اما عدد ۴ بر اعداد ۱، ۲ و ۴ قابل تقسیم بوده بنا براین عدد اول نمی باشد. عددی مانند ۴۵ پس از تجزیه به صورت حاصلضرب مقابل در می آید:
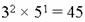
به این ترتیب در ساختار عدد ۴۵ دو عدد اول ۵ و ۳ مشاهده می شوند . بزرگترین عدد اول موجود در ۴۵ که دارای توان غیر صفراست عدد ۵ می باشد بنابراین عدد ۴۵ به محدوده ۵ تعلق دارد . در این محدوده اعداد اول کوچکتر از ۵ قرار می گیرند . مثال دیگر: در محدوده ۱۳ اعدادی قرار می گیرند که در ساختار خود اعداد اول ۳ ، ۵، ۷، ۱۱ و ۱۳ را شامل باشند. فاصله ای مانند ۲۶/۴۵ در محدوده ۱۳ می گنجند.
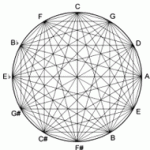
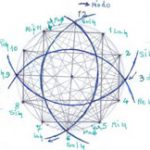
چرخه پنجم ها (دایره یا زنجیره پنجم ها) و سیستم فیثاغورثی
فاصله پنجم طبیعی ۲/۳(۷۰۱.۹۵۵ سنت) یکی از مهمترین فواصل بنیادی در سیستم فیثاغورثی و دومین فاصله خوش صدای آن است. با ایجاد یک چرخه Cycle یا زنجیره Chain از این فاصله می توان تمام فواصل مورد نیاز این سیستم را بدست آورد.به این فاصله٬ فاصله زاینده Generator می گوییم. باتوجه به کسر ۲/۳ که پس از تجزیه به این صورت تبدیل می شود:

می توان گفت که مدل فیثاغورثی در محدوده ۳ ۳-Limit می گنجد . فواصل ۲/۳ ٬ ۳/۴ ٬ ۸/۹ همگی فواصلی اند که در این محدوده قرار دارند. با توجه به نقش عدد ۳ ٬ می توان فواصل فیثاغورثی را به این فرم نمایش داد:
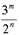
m می تواند مثبت یا منفی باشد که این امر نتیجه همان چرخه پنجم ها است. توان nام عدد ۲ همواره باید به گونه ای انتخاب شود تا نسبت کسر فواصل محدود به یک اکتاو بین ۱ و ۲ قرار گیرند. به عبارت دیگر:
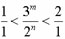
در کسر ۱/۲ و ۱/۱ توان ۳ صفر می باشد. به این ترتیب ۳ به توان ۳- معرف فاصله سوم کوچک فیثاغورثی ۲۷/۳۲ است:
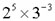































۱ نظر